Suppose that (mathcal{S}) is a surface in (mathbf{R}^{3}) with a parametrization (Phi) whose domain (mathcal{D}) is the

Question:

Suppose that $\mathcal{S}$ is a surface in $\mathbf{R}^{3}$ with a parametrization $\Phi$ whose domain $\mathcal{D}$ is the square in Figure 14. The values of a function $f$, a vector field $\mathbf{F}$, and the normal vector $\mathbf{N}=\mathbf{T}_{u} \times \mathbf{T}_{v}$ at $\Phi(P)$ are given for the four sample points in $\mathcal{D}$ in the following table. Estimate the surface integrals of $f$ and $\mathbf{F}$ over $\mathcal{S}$.

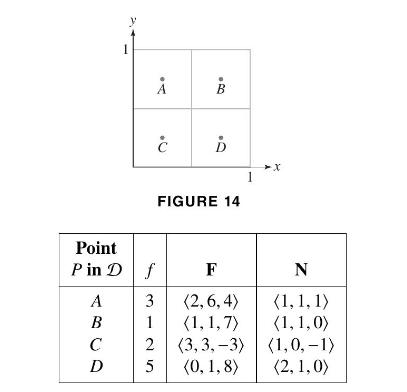
Point Pin D A B C D 1 A B f 3 1 2 5 D FIGURE 14 F (2,6,4) (1, 1,7) (3,3,-3) (0, 1, 8) X N (1, 1, 1) (1, 1,