Suppose (x) = x(2 + sin x) and let g(x) = x 2 + 1. Do (a) and (b) contradict LHopitals Rule? Explain. (a) Show

Suppose ƒ(x) = x(2 + sin x) and let g(x) = x² + 1.

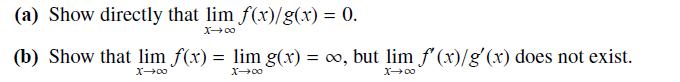
Do (a) and (b) contradict L’Hôpital’s Rule? Explain.

(a) Show directly that lim f(x)/g(x) = 0. X0 (b) Show that lim f(x) = lim g(x) = o, but lim f'(x)/g'(x) does not exist. X00 X0 X-00