The following problem was posed by Pierre de Fermat: Given three points A = (a₁, a₂), B = (b₁, b₂), and C = (c₁, c₂) in the plane, find the point P = (x, y) that minimizes the sum of the distances

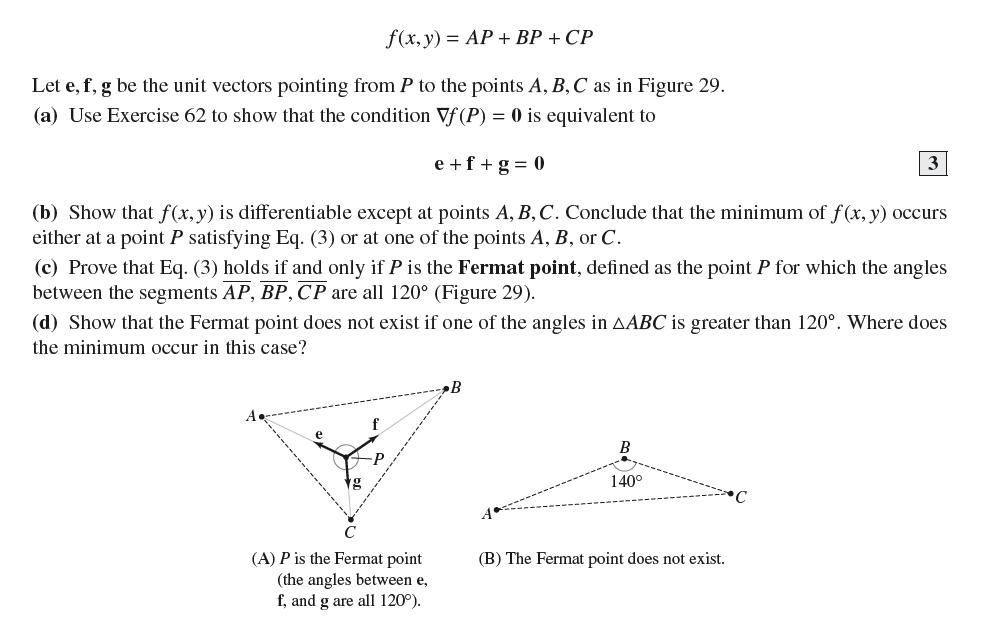
f(x, y) = AP + BP + CP Let e, f, g be the unit vectors pointing from P to the points A, B, C as in Figure 29. (a) Use Exercise 62 to show that the condition Vf (P) = 0 is equivalent to e + f +g=0 (b) Show that f(x, y) is differentiable except at points A, B, C. Conclude that the minimum of f(x, y) occurs either at a point P satisfying Eq. (3) or at one of the points A, B, or C. (c) Prove that Eq. (3) holds if and only if P is the Fermat point, defined as the point P for which the angles between the segments AP, BP, CP are all 120 (Figure 29). (d) Show that the Fermat point does not exist if one of the angles in AABC is greater than 120. Where does the minimum occur in this case? (A) P is the Fermat point (the angles between e, f, and g are all 120). B 3 B 140 (B) The Fermat point does not exist.