The gamma function, which plays an important role in advanced applications, is defined for n 1 by (a) Show that the integral defining (n)

The gamma function, which plays an important role in advanced applications, is defined for n ≥ 1 by

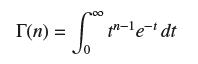
(a) Show that the integral defining Γ(n) converges for n ≥ 1 (it actually converges for all n > 0). Show that tⁿ⁻¹e^−t −2 for t sufficiently large.
(b) Show that Γ(n + 1) = nΓ(n) using Integration by Parts.
(c) Show that Γ(n + 1) = n! if n ≥ 1 is an integer. Use (b) repeatedly. Thus, Γ(n) provides a way of defining n-factorial when n is not an integer.

= 5 I(n) = t-le- dt