An improper integral I = a (x) dx is called absolutely convergent if a |(x)| dx converges. It can be shown

An improper integral I = ∫^∞_a ƒ(x) dx is called absolutely convergent if ∫^∞_a |ƒ(x)| dx converges. It can be shown that if I is absolutely convergent, then it is convergent.

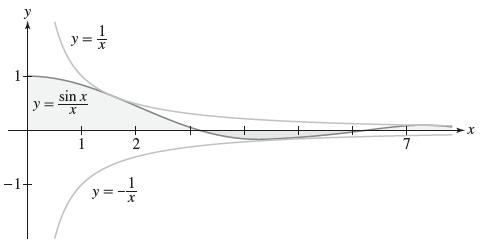
Let ƒ(x) = sin x/x and I = ∫^∞₀  ƒ(x) dx.We define ƒ(0) = 1. Then ƒ is continuous and I is not improper at x = 0.

(a) Show that

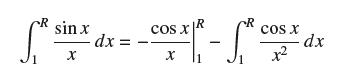
(b) Show that ∫^∞₁ (cos x/x²) dx converges. Conclude that the limit as R→∞of the integral in (a) exists and is finite.
(c) Show that I converges.
It is known that I = π/2. However, I is not absolutely convergent. The convergence depends on cancellation, as shown in Figure 13.

R R COS X COS X S * Sinx dx = cox x* - * cos x d. dx X X x