The Linear Approximation to (x) tan x at x 4 yields the estimate tan 4 h 1 2h Set K 6 2 and show, using a plot, that (x) K for x 4, 4 0 1 Then verify numerically that the error E satisfies Eq (5) for h 10 n , for 1 n 4 1 (x) E 2 VI

Question: The Linear Approximation to (x) = tan x at x = /4 yields the estimate tan /4 + h 1 2h. Set K

The Linear Approximation to ƒ(x) = tan x at x = π/4 yields the estimate tan π/4 + h − 1 ≈ 2h. Set K = 6.2 and show, using a plot, that |ƒ"(x)| ≤ K for x ∈ [π/4, π/4 + 0.1]. Then verify numerically that the error E satisfies Eq. (5) for h = 10⁻ⁿ, for 1 ≤ n ≤ 4.

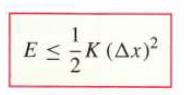
1 - (x)? E 2 VI

Step by Step Solution

★★★★★

3.31 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Let fx tan x Then f4 1 fx sec x and f4 2 Therefore by the Linear Approximation sh7tanh1 2h f ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

The following methods are standard ways of fault finding Programmable Logic Controller (PLC) programs: i. Watchdog timers Last output set ii. iii. Replication checks iv. Expected value checks Briefly...

Show that the Linear Approximation to f (x) = x at x = 9 yields the estimate 9 + h 3 1/6 h. Set K = 0.01 and show that |f(x)| K for x 9. Then verify numerically that the error E satisfies Eq. (5)...

Show that the Linear Approximation to (x) = x at x = 9 yields the estimate 9 + h 3 1/6 h. Set K = 0.01 and show that |"(x)| K for x 9. Then verify numerically that the error E satisfies Eq. (5)...

Calculus 3: Show work please! 14.4 Differentiability and tangent planes. 1. T Find an equation of the tangent plane at the given point. x, '9) = 7:, (4, 5) (Use symbolic notation and fractions where...

Hello tutor. I need help for these problems Exercises 3.9 Finding Linearizations X 12. f(x) =+ , a = 1.3 In Exercises 1-5, find the linearization L(x) of f(x) at x = a. 1. f(x) = x3 - 2x + 3, a = 2...

Calculus 3- Show work. 14.4Differentiabilityandtangentplanes: 1. Find an equation of the tangent plane at the given point. f (21,9) 2 % (4, 5) (Use symbolic notation and fractions where needed.) Find...

5. The following series of questions explores the relationship between the standard dot product on R" (geometry) and linear operators on R" (linear algebra). Let U be a n x n matrix, and think of it...

Downloaded 02/28/15 to 132.174.255.3. Redistribution subject to SIAM license or copyright; see http://www.siam.org/journals/ojsa.php 15.7. Exercises 475 changes and we laugh no more. While...

Least Squares Approximation Hector D. Ceniceros 1 Least Squares Approximation Let f be a continuous function on [a, b]. We would like to find the best approximation to f by a polynomial of degree at...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Cambria Limited took a $ 250,000 two- year note receivable from a customer in connection with a major inventory sale transaction on 1 January 20X5. The note required annual end- of- year interest...

How should prior period adjustments be reported in the financial statements? Give an example of a prior period adjustment.

Edawrds had decided to use monetary unit sample in the audit

Cross-Cultural Awareness. Think about a cross-cultural situation that you have been in or are currently in (a situation in which you are working with or negotiating with people from another culture)....

Compute the following derivatives using the chain rule. A(z) = ln(1 + ez).

Compute the following derivatives using the chain rule. G(s) = 8ex2.

Compute the following derivatives using the chain rule. s(w) = 4.21 + ew.

Ten annual returns are listed in the following table:(Click on the following icon in order to copy its contents into a spreadsheet.) 19.9% 16.6% 18.0% 50.0% 43.3% 1.2% 16.5% 45.6% 45.2% 3.0% a. What...

Discuss what your group thought of using drones and CountThings software for counting inventory. What are some pros and cons of this method (The example in the second video uses a photo with a few...

N Maxwell Company uses a standard cost accounting system and applies production overhead to products on the basis of machine hours. The following information is available for the year just ended:...