This exercise proves the Chain Rule without the special assumption made in the text. For any number b, define a new function

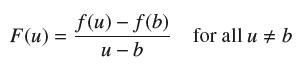
(a) Show that if we define F(b) = ƒ'(b), then F is continuous at u = b.
(b) Take b = g(a). Show that if x ≠ a, then for all u,

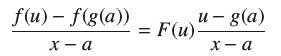
Note that both sides are zero if u = g(a).

(c) Substitute u = g(x) in Eq. (1) to obtain

Eq.(1)

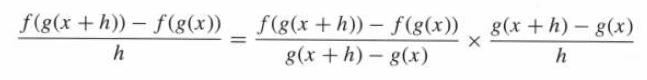
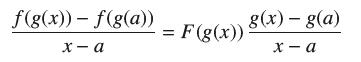
Derive the Chain Rule by computing the limit of both sides as x → a.

F(u): = f(u) - f(b) u-b for all u b