This exercise shows that there exists a function that is not differentiable at (0, 0) even though all directional derivatives at (0, 0) exist. Define ƒ(x, y) = x²y/(x² + y²) for (x, y) ≠ 0 and ƒ(0, 0) = 0.
(a) Use the limit definition to show that D_v ƒ(0, 0) exists for all vectors v. Show that ƒx(0, 0) = ƒy(0, 0) = 0.
(b) Prove that ƒ is not differentiable at (0, 0) by showing that Eq. (7) does not hold.

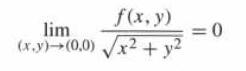
lim (x,y)(0,0) f(x, y) x + y =0