Question: Two paths r 1 (t) and r 2 (t) intersect if there is a point P lying on both curves. We say that r 1
Two paths r1(t) and r2(t) intersect if there is a point P lying on both curves. We say that r1(t) and r2(t) collide if r1(t0) = r2(t0) at some time t0.
Determine whether r1(t) and r2(t) collide or intersect, giving the coordinates of the corresponding points if they exist:
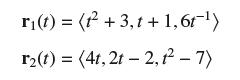
r(t) = (+ 3,1 + 1,6t-) r2(t) = (4t, 2t 2, 1-7) -
Step by Step Solution
3.36 Rating (159 Votes )
There are 3 Steps involved in it
To determine if the paths ... View full answer

Get step-by-step solutions from verified subject matter experts


