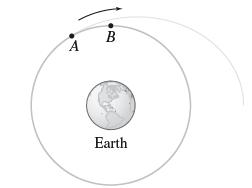
Two space shuttles A and B orbit the earth along the solid trajectory in Figure 9. Hoping to catch up to B, the pilot of A applies a forward thrust to increase her shuttle’s kinetic energy. Use Exercise 20 to show that shuttle A will move off into a larger orbit as shown in the figure. Then use Kepler’s Third Law to show that A’s orbital period T will increase (and she will fall farther and farther behind B)!

Data From Exercise 20

Show that a planet in an elliptical orbit has total mechanical energy E = −GMm/2a, where a is the semimajor axis. Use Exercise 19 to compute the total energy at the perihelion.

Data From Exercise 19

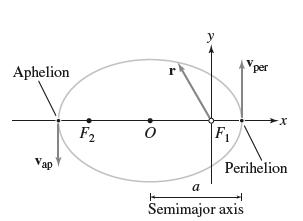
The perihelion and aphelion are the points on the orbit closest to and farthest from the sun, respectively (Figure 8). The distance from the sun at the perihelion is denoted r_per and the speed at this point is denoted v_per. Similarly, we write r_ap and v_ap for the distance and speed at the aphelion. The semimajor axis is denoted a.

Prove that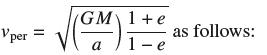

(a) Use Conservation of Energy (Exercise 17) to show that

Data From Exercise 17

The total mechanical energy (kinetic energy plus potential energy) of a planet of mass m orbiting a sun of mass M with position r and speed v = ΙΙr'ΙΙ is

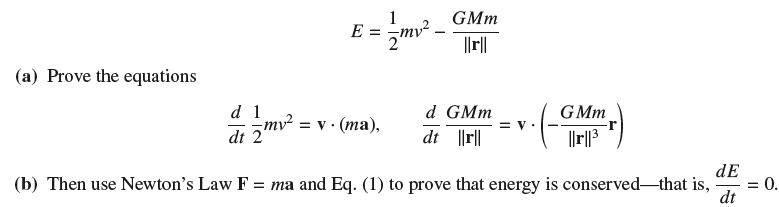
(b) Show that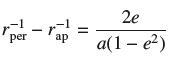using Exercise 13. 

Data From Exercise 13

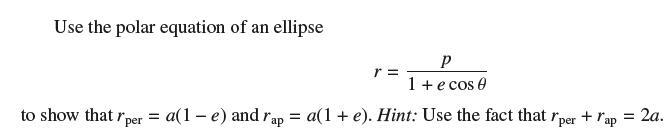
(c) Show that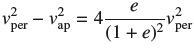 using Exercise 15. Then solve for vper using (a) and (b).

Data From Exercise 15

A B Earth