Question: Two vector-valued functions r 1 (s) and r 2 (s) are said to agree to order 2 at s 0 if ri (So) = r(so),

Two vector-valued functions r₁(s) and r₂(s) are said to agree to order 2 at s₀ if

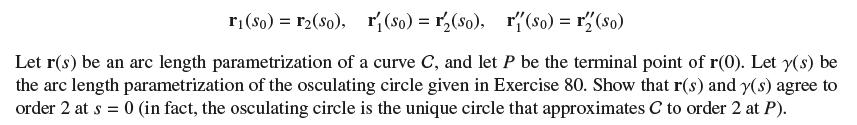
r(So) = r(So), r(so) = r(so), r(so) = r (so) Let r(s) be an arc length parametrization of a curve C, and let

ri (So) = r(so), r (so) = r(so), r(so) = r2(so) Let r(s) be an arc length parametrization of a curve C, and let P be the terminal point of r(0). Let y(s) be the arc length parametrization of the osculating circle given in Exercise 80. Show that r(s) and y(s) agree to order 2 at s = 0 (in fact, the osculating circle is the unique circle that approximates C to order 2 at P).

Step by Step Solution

★★★★★

3.50 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

KYC's stock price can go up by 15 percent every year, or down by 10 percent. Both outcomes are equally likely. The risk free rate is 5 percent, and the current stock price of KYC is 100. (a) Price a...

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Please quality check my solutions for this advanced heat transfer problem. Show all work. Thank you. All original documents are located at the bottom. 3.9 COMPACT HEAT EXCHANGERS 3.9.10-1 3.9.10...

U.S. Copyright Law (title 17 of U.S. code) governs the reproduction and redistribution of copyrighted material. Downloading this document for the purpose of redistribution is prohibited. Chapter 15...

5. Risk-adjusted discount ratesBasic Country Wallpapers is considering investing in one of three mutually exclusive projects, E, F, and G. The firm's cost of capital, r, is 14.8%, and the risk-free...

Consider the relation schema R = (N, Y, P, M, C) and assume that the following set of functional dependencies hold on R: F = { N M, NY P, M C} Use the algorithm example below for question 2. 2. Use...

Lab-8 (LK) Parallel Circuit (3) Light Bulbs and Sockets Transistor socket 3.30 Resistor Potentiometer Objective Iran core) 1. Learn to build up a parallel circuit with three resistors and one DC...

Hello, I am having some troubles understanding the formulas for corporate finance on this document. I would be great to have someone who could explain them to me with some practical examples. Thanks...

Let s : {1,2,...,n} {1,2,...,n} be a function of sets that is invertible. Such a map determines a linear transformation S : Rn Rn given by S(ei) = es(i), and we call such linear maps S permutations....

What kind of deformation does a cube of Jell-O exhibit when it jiggles?

Show that if f and g are both positive increasing functions on interval I then their product FG is increasing on I

1 0 of 1 6 Concepts completed iltiple Choice Question tching from one segment of the bond market to another is called It is pursued when an irmestor believes the yield spread between two wectors of...

Go to a local business or organization and ask to speak for a few minutes with a supervisor about organizational management concepts.? P-987

An application of Kirchhoffs Rules to the circuit shown results in the following system of equations: Find the currents I 1 , I 2 , I 3 and I 4 . -4 + 8 212 = 0 8 = 514 + I1 4 = 313 + I1 I3 + I4 =...

To manufacture an automobile requires painting, drying, and polishing. Epsilon Motor Company produces three types of cars: the Delta, the Beta, and the Sigma. Each Delta requires 10 hours (hr) for...

A Florida juice company completes the preparation of its products by sterilizing, filling, and labeling bottles. Each case of orange juice requires 9 minutes (min) for sterilizing, 6 min for filling,...

Grant Corporation is looking to purchase a building costing $930,000 by paying $315,000 cash on the purchase date, and agreeing to make payments every three months for the next five years. The first...

Came U'Lake, keed A. Green, and Uoug A. UNot share a passion tor goit and decide to go into the goit club manufacturing business together. On January 2, 2022, D'Lake, Green, and Divot form the...

Which of the following is not an example of a direct materials cost? A) tires on a bicycle B) engine in a car C) shelves on a bookcase D) nails used to manufacture a desk