Question: Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. C x y d x + ( x 2

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated.

THEOREM 1 Green's Theorem Let D be a domain whose boundary 3D

$\int_{C} x y d x + (x^{2} + x) d y$ , where $C$ is the path in Figure 17

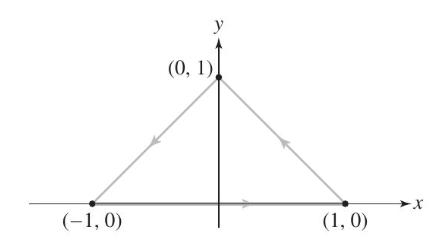
is a simple closed curve, oriented counterclockwise. If F and F have

THEOREM 1 Green's Theorem Let D be a domain whose boundary 3D is a simple closed curve, oriented counterclockwise. If F and F have continuous partial deriva- tives in an open region containing D, then $o F1 dx + F2 dy 1 (F2-F) da dA = ay 2

Step by Step Solution

★★★★★

3.38 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

SOLUTION Let D be the given path together with its interior In the given function P x y a... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. Let $\mathbf{F}(x, y)=\left\langle 2 x e^{y}, x+x^{2} e^{y}ightangle$ and let $C$...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. The line integral of $\mathbf{F}(x, y)=\left\langle e^{x+y}, e^{x-y}ightangle$ along...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. $\oint_{C} \mathbf{F} \cdot d \mathbf{r}$, where \(\mathbf{F}(x, y)=\left\langle...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. $\oint_{C} 5 y d x+2 x d y$, where $C$ is the triangle with vertices...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. $\oint_{C} e^{2 x+y} d x+e^{-y} d y$, where $C$ is the triangle with vertices...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. $\oint_{C} y^{2} d x+x^{2} d y$, where $C$ is the boundary of the square \(-1 \leq...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. $\oint_{C} y^{2} d x+x^{2} d y$, where $C$ is the boundary of the square that is...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. $\oint_{C} \mathbf{F} \cdot d \mathbf{r}$, where \(\mathbf{F}(x, y)=\left\langle x+y,...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. $\oint_{C} x^{2} y d x$, where $C$ is the unit circle centered at the origin...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwise indicated. (In a+y)da- a'dy, where is the rectangle with vertices (1, 1), (3, 1), (1, 4), and (3,...

Sabel Co. purchased assembly equipment for $500,000 on January 1, 2016. Sabels financial condition immediately prior to the purchase is shown in the following horizontal statements model: The...

Identify the C3H5Br isomers on the basis of the following information: (a) Isomer A has the 1H NMR spectrum shown in Figure 13.40.

63. GPS Usage in Canada. According to CNN, 55% of all U.S. smartphone users have used their GPS capability to get directions. Suppose a major provider of wireless telephone service in Canada wants to...

How do leadership characteristics help managers do their work?

The density function f(x) = e 3-x /(1 + e 3-x ) 2 is an example of a logistic distribution. (a) Verify that f is a probability density function. (b) Find P(3

Let f (x) = c/(1 + x 2 ). (a) For what value of c is f a probability density function? (b) For that value of c, find P (-1

An online retailer has determined that the average time for credit card transactions to be electronically approved is 1.6 seconds. (a) Use an exponential density function to find the probability that...

A company is considering the purchase of a new machine for $83,160. Management predicts that the machine can produce sales of $21,000 each year for the next 10 years. Expenses are expected to include...

What is data mining? Police conducting a full scope background check of a suspect, which includes questioning family and neighbors A technique used by police to access a suspect's computer, bypass...

On January 1, 2024, Blossom Retailers had inventory of $48,700. On December 31, 2024, total inventory on hand was $64,700 Blossom reported the following account balances on December 31: 14 Freightin...