Question: Use the differential equation for a leaking container, Eq. (3). At t = 0, a conical tank of height 300 cm and top radius 100

Use the differential equation for a leaking container, Eq. (3).

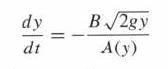
dy dt B 2gy A(y)

At t = 0, a conical tank of height 300 cm and top radius 100 cm [Figure 11(A)] is filled with water. Water leaks through a hole in the bottom of area B = 3 cm2. Let y(t) be the water level at time t.

(a) Show that the tank’s cross-sectional area at height y is A(y) = π/9y².
(b) Solve the differential equation satisfied by y(t).
(c) How long does it take for the tank to empty?

300 cm 100 cm Hole (A) Conical tank y Radius 4 m 15 m Hole (B) Horizontal tank

dy dt B 2gy A(y)

Step by Step Solution

★★★★★

3.45 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a By similar triangles the radius r at height y satisfie... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Use the differential equation for a leaking container, Eq. (3). A tank has the shape of the parabola y = x 2 , revolved around the y-axis. Water leaks from a hole of area B = 0.0005 m 2 at the bottom...

Use the differential equation for a leaking container, Eq. (3). Water leaks through a hole of area B = 0.002 m 2 at the bottom of a cylindrical tank that is filled with water and has height 3 m and a...

Use the differential equation for a leaking container, Eq. (3). A tank has the shape of the parabola y = ax2 (where a is a constant) revolved around the y-axis. Water drains from a hole of area B m2...

a. Question 2 Consider an inverted conical tank (with radius R and height It) as shown in the Cure below. The tani tank is being filled with water and inlet now rate is 100 ml/min and the initial...

Hello, you already did chapter 1 and 2 of my MASTERS Thesis already for me. (See attached) So normally you know masters thesis consist of 5 chapters right ??..... But in this case my thesis will be 4...

M MyOpenMath X + V X -> C A https://www.myopenmath.com/assess2/?cid=161294&aid=11474925#/full GE MyApps - Login S Blackboard & Webmail S Seneca College - H... S. Seneca Libraries On... S ITS Seneca...

Section 6.5 Reading Assignment: Work and Fluid Forces Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions very...

1. It has been said that a smartphone is a microcomputer in your hand. Discuss the security implications of this statement. 2. What management, organizational, and technology issues must be addressed...

[The following information applies to the questions displayed below.) Walton Company makes and sells products with varlable costs of $24 each. Walton incurs annual fixed costs of $441,160. The...

As the price of the underlying asset decreases, the put buyer's potential profit Multiple choice question. is small. increases to a limit . is completely unlimited. is large.

To conduct a valid regression analysis, both x and y must be approximately normally distributed. LO.1

In problem, find the exact values of the six trigonometric functions of the given angle. If any are not defined, say not defined. Do not use a calculator. /6

In problem, find the exact values of the six trigonometric functions of the given angle. If any are not defined, say not defined. Do not use a calculator. /3

In problem, find the exact values of the six trigonometric functions of the given angle. If any are not defined, say not defined. Do not use a calculator. -135

18. What is the maximum depreciation in 2016 for a new computer acquired on July 2, 2016, for $3,000? The computer is the only property placed in service in 2016. It is used 40% for business and 60%...

You are given the following Intel assembly program. Give the contents of the EAX, EBX, ECX, EDX, EBP, ESP registers and the stack at the locations in the program marked as BP 1 , BP 2 , BP 3 , BP 4 ,...

Suppose that Microsoft issued a bond with 5 years until maturity, face value of $10,000, coupon rate of 5% ( annual payments). The yield to maturity when it was issued was 4%. What was the price of...