a. Consider the number 0.555555 . . ., which can be viewed as the series 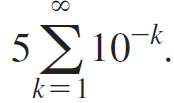Evaluate the geometric series to obtain a rational value of 0.555555 . .

b. Consider the number 0.54545454 . . ., which can be represented by the series 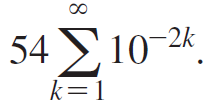Evaluate the geometric series to obtain a rational value of the number. 

c. Now generalize parts (a) and (b). Suppose you are given a number with a decimal expansion that repeats in cycles of length p, say, n₁, n₂ . . . , n_p, where n₁, . . . ,n_p are integers between 0 and 9. Explain how to use geometric series to
obtain a rational form for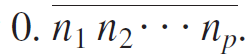

d. Try the method of part (c) on the number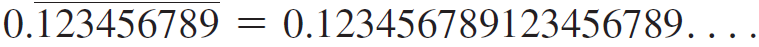

e. Prove that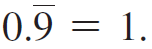

-k 510. k=1 54 10-24. k=1