a. Sketch the function f(x) = 1/x on the interval [1, n + 1], where n is a positive integer. Use this graph to verify that

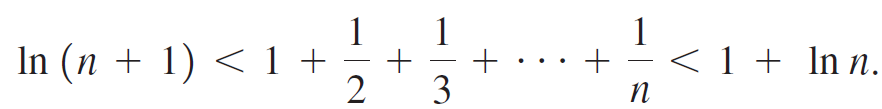
b. Let S_n be the sum of the first n terms of the harmonic series, so part (a) says ln (n + 1) < S_n < 1 + ln n. Define the new sequence {E_n} by 

E_n = S_n - ln (n + 1), for n = 1, 2, 3, . . . Show that E_n > 0, for n = 1, 2, 3,  . . .

c. Using a figure similar to that used in part (a), show that

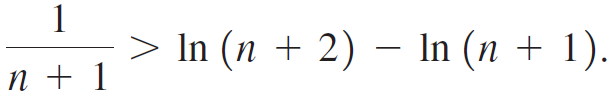
d. Use parts (a) and (c) to show that {E_n} is an increasing sequence (E_{n + 1} > E_n).

e. Use part (a) to show that {E_n} is bounded above by 1.

f. Conclude from parts (d) and (e) that {E_n} has a limit less than or equal to 1. This limit is known as Euler’s constant and is denoted γ (the Greek lowercase gamma).

g. By computing terms of {E_n}, estimate the value of γ and compare it to the value γ ≈ 0.5772. (It has been conjectured that γ is irrational.)

h. The preceding arguments show that the sum of the first n terms of the harmonic series satisfy S_n ≈ 0.5772 + ln (n + 1). How many terms must be summed for the sum to exceed 10?

1 In (n + 1) < 1 + 1 1 < 1 + In n. > In (n + 2) In (n + 1). n + 1