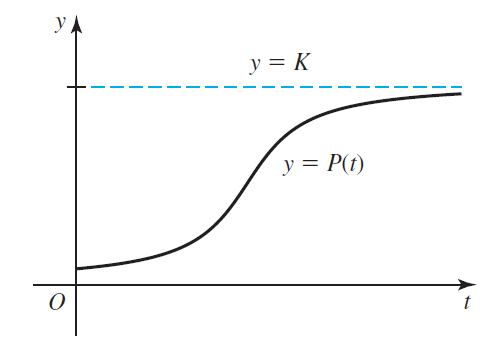
Scientists often use the logistic growth function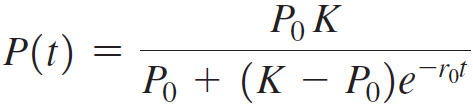to model population growth, where P₀ is the initial population at time t = 0, K is the carrying capacity, and r₀ is the base growth rate. The carrying capacity is a theoretical upper bound on the total population that the surrounding environment can support. The figure shows the sigmoid (S-shaped) curve associated with a typical logistic model.

The population of the world reached 6 billion in 1999 (t = 0). Assume Earth’s carrying capacity is 15 billion and the base growth rate is r₀ = 0.025 per year.

a. Write a logistic growth function for the world’s population (in billions) and graph your equation on the interval 0 ≤ t ≤ 200 using a graphing utility.

b. What will the population be in the year 2020? When will it reach 12 billion?

PoK P(t) Po + (K Po)ero* y, y = K y = P(t)