Suppose that a light source at A is in a medium in which light travels at speed v₁ and the point B is in a medium in which light travels at speed v₂ (see figure). Using Fermat’s Principle, which states that light travels along the path that requires the minimum travel time (Exercise 65), show that the path taken between points A and B satisfies (sin θ₁)/v₁ = (sin θ₂)/v₂.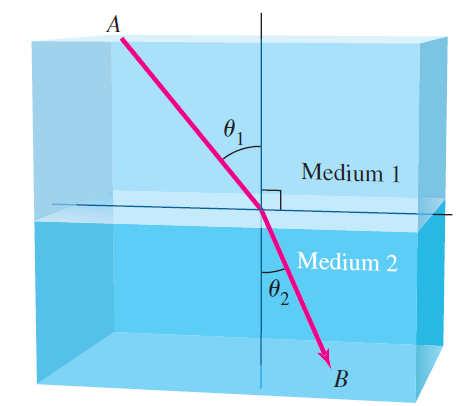

Data from Exercise 65

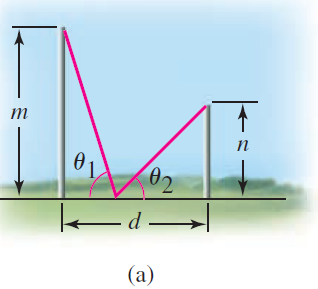
Two poles of heights m and n are separated by a horizontal distance d. A rope is stretched from the top of one pole to the ground and then to the top of the other pole. Show that the configuration that requires the least amount of rope occurs when θ₁ = θ₂ (see figure).

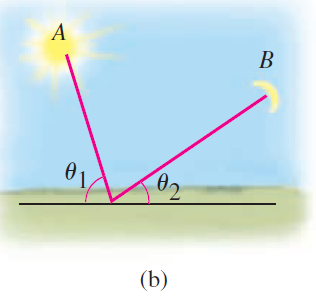
Fermat’s Principle states that when light travels between two points in the same medium (at a constant speed), it travels on the path that minimizes the travel time. Show that when light from a source A reflects off a surface and is received at point B, the angle of incidence equals the angle of reflection, or θ₁ = θ₂ (see figure).

Medium 1 Medium 2 B 02 -d (a)