Suppose you approximate f(x) = sec x at the points x = -0.2, -0.1, 0.0, 0.1, and 0.2 using the Taylor polynomials p₂(x) = 1 + x²/2 and p₄(x) = 1 + x²/2 + 5x⁴/24. Assume that the exact value of sec x is given by a calculator. 

a. Complete the table showing the absolute errors in the approximations at each point. Show two significant digits.

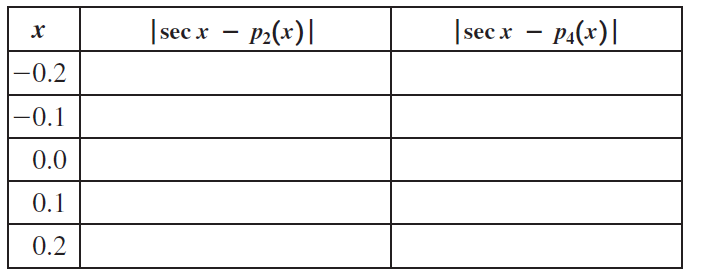
b. In each error column, how do the errors vary with x? For what values of x are the errors largest and smallest in magnitude?

|sec x - p.(x)|| |sec x P:(x)| |-0.2 |-0.1 0.0 0.1 0.2