Question: In Exercises 6568 in the previous section, we saw that Newtons Law of Cooling states that the rate of change of the temperature of an

In Exercises 65–68 in the previous section, we saw that Newton’s Law of Cooling states that the rate of change of the temperature of an object is proportional to the difference in temperature between the object and the surrounding medium. This leads to the differential equation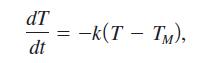 dT dt || -K(T-TM),

where T is the temperature of the object after time t, T_M is the temperature of the surrounding medium, and k is a constant. In the previous section, we solved this equation by separation of variables. Show that this equation is also linear, and find the solution by the method of this section.

Exercises 66

According to the solution of the differential equation for Newton’s law of cooling, what happens to the temperature of an object after it has been in a surrounding medium with constant temperature for a long period of time? How well does this agree with reality?

dT dt || -K(T-TM),

Step by Step Solution

★★★★★

3.36 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Multiply both sid... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus With Applications Questions!

Newtons law of cooling states that the rate of change of temperature of an object is proportional to the difference in temperature between the object and the surrounding medium. Thus, if T is the...

The drag on a falling object is proportional to the square of its speed. In a differential equation where v is speed, a is acceleration, and D is drag. Suppose that a = 9.8 m/s2 and that D = 0.0032...

Its Math 307 class and about the differential equation 8. + 2/4 points Previous Answers My Notes Newton's law of cooling states that the temperature of an object changes at a rate proportional to the...

Previous Problem Problem List Next Problem (1 point) Newton's law of cooling states that the temperature of an object changes at a rate proportional to the difference between its temperature and that...

Lesson 9 Applications of First Order: Problem 6 Previous Problem Problem List Next Problem (1 point) Newton's law of cooling states that the temperature of an object changes at a rate proportional to...

#9. Consider triangle ABC drawn in a circle of radius 6 cm with vertex C at the centre of the circle, as shown. Determine the angle O that maximizes the area of the triangle. (Make sure you verify...

Please need an answer asap A thermometer is taken from a room where the temperature is 24C to the outdoors, where the temperature is -10C. After one minute the thermometer reads 13"C. (a) What will...

Answer the following question. Follow the format given and write legibly to avoid confusions of answer. THANK YOU VERY MUCH!! 1. Find the general solution of the given differential equation, and use...

A curve passes through the point (0,5) and has the property that the slope of the curve at every point P is four times the y-coordinate of P. What is the equation of the curve? y(x) = ngs Newton's...

Manpower Electric Company has 6 percent convertible bonds outstanding. Each bond has a $1,000 par value. The conversion ratio is 20, the stock price $36, and the bonds mature in 16 years. a. What is...

A freight forwarder has determined that a ocean and inland transit time from Tokyo, japan to Berlin, Germany is approximately 30 to 33 days on average. Her customer finds the cost acceptable, but the...

Exercise 1 2 - 1 7 ( Algorithmic ) ( LO . 2 ) Compute the 2 0 2 4 AMT exemption for the following taxpayers: Round final answer to the nearest dollar. If an amount is zero, enter " 0 " . Click here...

Give four reasons why a business rules approach is advocated as a new paradigm for specifying information systems requirements.

Perform the indicated operations. (6m + 5)(6m 5)

Write each rational expression in lowest terms. (6y 2 + 11y + 4)/(3y 2 + 7y + 4)

Factor each polynomial. If a polynomial cannot be factored, write prime. Factor out the greatest common factor as necessary. y 2 4yz 21z 2

CASE 5-1 You are the Chief Financial Officer (CFO) for Zen Distributors, Inc., a media broker that secures shelf space in independent bookstores for small publishing companies. As a member of the...

Bird's Eye Treehouses, Inc., a Kentucky company, has determined that a majority of its customers are located in the Pennsylvania area. It therefore is considering using a lockbox system offered by a...

Kurnick Company expects that the pound will depreciate from $1.70 to $1.68 in one year. it has no money to invest, but it could borrow money to invest.It has been approved by a bank to borrow either...