Its Math 307 class and about the differential equation

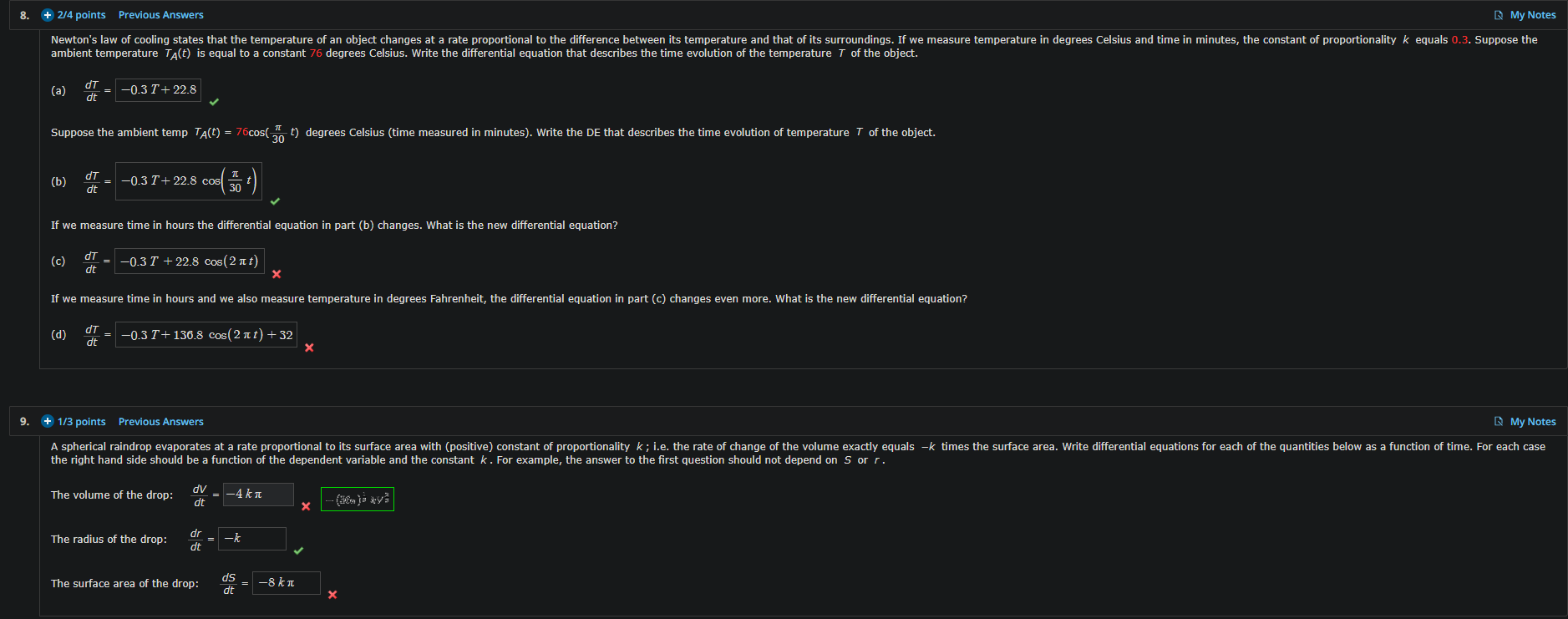
8. + 2/4 points Previous Answers My Notes Newton's law of cooling states that the temperature of an object changes at a rate proportional to the difference between its temperature and that of its surroundings. If we measure temperature in degrees Celsius and time in minutes, the constant of proportionality k equals 0.3. Suppose the ambient temperature TA(t) is equal to a constant 76 degrees Celsius. Write the differential equation that describes the time evolution of the temperature 7 of the object. (a) -0.3 7 + 22.8 Suppose the ambient temp TA(t) = 76cos(2 t) degrees Celsius (time measured in minutes). Write the DE that describes the time evolution of temperature 7 of the object. (b) dt - -0.3 7+22.8 cos 30 If we measure time in hours the differential equation in part (b) changes. What is the new differential equation? (c) di dt -0.3 7 + 22.8 cos(2 n t) If we measure time in hours and we also measure temperature in degrees Fahrenheit, the differential equation in part (c) changes even more. What is the new differential equation? (d) dt -0.3 7+136.8 cos(2 n t) + 32 . + 1/3 points Previous Answers My Notes A spherical raindrop evaporates at a rate proportional to its surface area with (positive) constant of proportionality k ; i.e. the rate of change of the volume exactly equals -k times the surface area. Write differential equations for each of the quantities below as a function of time. For each case the right hand side should be a function of the dependent variable and the constant k . For example, the answer to the first question should not depend on S or r . The volume of the drop: dv dt -4 kn X The radius of the drop: dr dt -K The surface area of the drop: dt -8 kn