Question: Let f(x) be a continuous function with f(x) 0 for a x b. Let R be the region with area A that

Let f(x) be a continuous function with f(x) ≥ 0 for a ≤ x ≤ b. Let R be the region with area A that is bounded by the curve y = f(x), the x axis, and the lines x = a and x = b. Then the centroid (or center) of R is the point (x̅, y̅), where

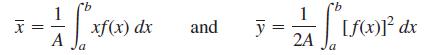
X 7 - = - 1x A a xf(x) dx and y

In Exercises 65 and 66, find the centroid of the region shown. You may need to use one or more formulas from Table 6.1.

= Life a 2A [f(x)] dx

X 7 - = - 1x A a xf(x) dx and y = Life a 2A [f(x)] dx

Step by Step Solution

★★★★★

3.59 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

So the centroid is 0244 0353 In 2 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus With Applications Questions!

In Exercises 1-3, determine whether the given matrix is in row echelon form. If it is, state whether it is also in reduced row echelon form. 1. 2. 3. 130 001 100 040 110 700 0 0 0 1

Let f(x) be a continuous function with f(x) 0 for a x b. Let R be the region with area A that is bounded by the curve y = f(x), the x axis, and the lines x = a and x = b. Then the centroid (or...

The shaded region shown in the accompanying figure is a parking lot for a shopping mall. The dimensions are in hundreds of feet. To improve parking security, the mall manager plans to place a...

Let a > 0 and let f: [-a, a] - R be a continuous function that is piecewise continuously differen- tiable on (-a, a). Assume that f(x) 2 0 for all x E [-a, a] and f(-a) = f(a) = 0. Let A be the area...

(a) Consider the function f : R - R defined by 2 if x 0. (i) Prove that f is discontinuous at 0. [3] (ii) Using only the definition of continuity, prove that f is continuous at every c 0. [5] (b)...

MACM 316 - Assignment 7 Please read the Guidelines for Assignments first. Submit a one-page PDF report to Canvas and upload you Matlab scripts (as m-files). Do not use any other file formats. Keep in...

3. Let f be a continuous single-variable function defined on [0, 1], and let D be the region in R2 bounded by x = 0, y = 0, and y = 1 - r. Show that f(x + y)dA = uf(u)du. Your answer must work for D...

textbroker.com X Final Exam Canvas LMS X MATH140-12141 (ONL) X BusCalc.pdf X *Dashboard X C D File | /Users/davidorozco/Downloads/MathG140FinalExam-Summer2023%20(1).pdf Update : Suggested Sites M...

1. [10 points] A car is traveling on a long straight road. The driver suddenly realizes that there is a stop sign exactly 40 feet in front of the car and immediately hits the brakes. The car's...

An octave contains twelve distinct notes (on a piano, five black keys and seven white keys). How many different eight-note melodies within a single octave can be written if the black keys and white...

Assume the price of gas across gas stations in Boston at any particular time has a normal distribution with unknown mean and variance. In order to estimate the expected price on a given day, you...

15. The total utilities associated with the first 5 units of consumption of good X are 15, 30, 40, 47, and 50, respectively. What is the marginal utility associated with the third unit? a. 15 b. 70...

List one of the facultys publications in APA style.

Provide a stem-and-leaf plot of the age at first sperm-positive urine specimen? Pediatrics, Endocrinology A study was performed among 40 boys in a school in Edinburgh to look at the presence of...

What will be the revised sample size estimate in Problem 10.44 if the lack of compliance is taken into account? Investigators expect that not all participants will comply. In particular, they project...

Which nonparametric test should be used to test the hypothesis that the mean SBPs for the two machines are comparable? Hypertension An instrument that is used in some blood-pressure studies is the...

Amanda would like to organize BAL as either an LLC (taxed as a sole proprietorship) or a C corporation. In either form, the entity is expected to generate an 8 percent annual before-tax return on a...

name and fully explain three procedural protections given to someone who has been accused of a crime? BRIEF PROBLEMS (10 points each) You must answer ALL of the following questions. The use of...

Timberlines Ltd is a large forestry company which grows and harvests trees and transports them to its mills where the timber is pulped (an operation which uses a great deal of water and produces an...