The grooves or tread in a tire occasionally pick up small pieces of gravel, which then are often thrown into the air as they work loose from the tire. When following behind a vehicle on a highway with loose gravel, it is possible to determine a safe distance to travel behind the vehicle so that your automobile is not hit with flying debris by analyzing the function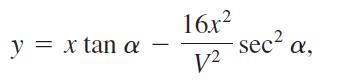

where y is the height (in feet) of a piece of gravel that leaves the bottom of a tire at an angle α relative to the roadway, x is the horizontal distance (in feet) of the gravel, and V is the velocity of the automobile (in feet per second).

(a) If a car is traveling 30 mph (44 ft per second), find the height of a piece of gravel thrown from a car tire at an angle of π/4, when the stone is 40 ft from the car.
(b) Putting y = 0 and solving for x gives the distance that the gravel will fly. Show that the function that gives a relationship between x and the angle a for y = 0 is given by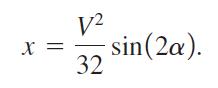

(c) Using part (b), if the gravel is thrown from the car at an angle of π/3 and initial velocity of 44 ft per second, determine how far the gravel will travel.
(d) Find dx/dα and use it to determine the value of a that gives the maximum distance that a stone could fly.
(e) Find the maximum distance that a stone can fly from a car that is traveling 60 mph.

y = x tan a - 16x - sec a, V