Cell counts y ij in an I J contingency table have a multinomial (n ij ) distribution Show that P(Y ij n ij ), i 1, , I, j 1, , J can be expressed as where ij ij IJ IJ IJ and d is a constant independent of the data Find an alternative expression using local odds ratios ij , by showing that 1 1 J 1 d n (n ')' ep nlog(,) i 1 j 1 1 I 1 J 1 n4 og( ) n log( ) j log( u) i 1 j 1

Question: Cell counts {y ij } in an I J contingency table have a multinomial (n; { ij }) distribution. Show that {P(Y ij =

Cell counts {y_ij} in an I × J contingency table have a multinomial (n; {π_ij}) distribution. Show that {P(Y_ij = n_ij), i = 1,..., I, j = 1,..., J} can be expressed as

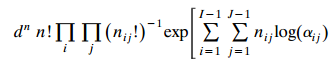
1-1 J-1 d" n! (n;')' ep| nlog(,) i=1 j=1 -1 I-1 J-1

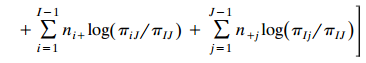
+ n4 og( / ) + n.log( / ) j log( /

where α_ij = π_ij π_IJ/π_IJ π_IJ and d is a constant independent of the data. Find an alternative expression using local odds ratios {θ_ij}, by showing that

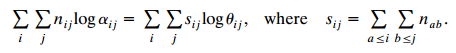
u) i=1 j=1

1-1 J-1 d" n! (n;')' ep| nlog(,) i=1 j=1 -1 I-1 J-1 + n4 og( / ) + n.log( / ) j log( / u) i=1 j=1

Step by Step Solution

★★★★★

3.43 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To show the expression for the probabilities in a multinomial distribution and the altern... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Categorical Data Analysis Questions!

In some situations where the expected cell counts are too small, as in the case of the grades given by Professors Alpha and Beta in Exercise 43, we can complete an analysis anyway. We can often...

Suppose that each student in a sample had been categorized with respect to political views, marijuana usage, and religious preference, with the categories of this latter factor being Protestant,...

The table shows GSS data on happiness and the number of close friends, with expected cell counts given underneath the observed counts. a. Suppose the variables were independent. Explain what this...

In an I J contingency table, let ij denote local odds ratio (2.10), and let ij denote its sample value. a. show that asymp. cov(n log ij , n log i+1, j ) = [ 1 i+1, j + 1 i+1, j+1 ]. b. Show...

The best definition for nonparametric statistics I can think of is when data does not fit inside the normal parameters of a normal distribution, it calls for the use of this statistical method....

15. Chi-Squared Test BA2606-05 (X2 Test) 1 Two Techniques... The first is a [ applied to data produced by a multinomial experiment, a generalization of a binomial experiment and is used to describe...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

This week, we are going to do learn how to summarize categorical data using Rguroo. We will also learn how to upload a dataset from a text file into Rguroo. For this problem set we will use the...

Alden's unit cost on the five-speed blender is $32. Alden's desired retum on sales is 20 percent. What is Alden's markup price?

Currently, a callable bond is selling for $1,145. It pays a 8% semi-annual coupon, has a 14-year maturity, and a $1,000 par value, but it can be called in 5 years at $1.050. Assume that no costs...

Income Statement Income Gross sales 5 Sales returns and allowances 240000 Net sales 6660000 Cost of goods sold 2760000 Gross profit 3900000 Dividends received from stock investments in lessthan20...

=+5. In 1982 Robert Crandell, CEO of American Airlines, phoned the Braniff Airways CEO and said, "Raise your fares 20 percent and I'll raise mine the next moming."

Do very short parents tend to have children who are even shorter, or short but not as short as they are? Explain, identifying the response and explanatory variables and the role of regression toward...

The FL Crime data file on the text CD contains data for all counties in Florida on y = median annual income (thousands of dollars) for residents of the county and x = percent of residents with at...

For the House Selling Prices FL data set on the text CD, when we regress y = selling price (in dollars) on x = number of bedrooms, we get the results shown in the printout. a. One home with three...

Home / Courses IENCE 623.(SUMMER VAN-18) 1 Week 1 troduction Mini Our Percentage Change + Back to Week 1 Introduction On5 Maddef 100 You want to qualify for the 20% quarterly sales bonus at work. You...

STA 210 - Homework 11 Section IV. B. and Lab 11 Section IV. B. Questions 1) What is the z used to create a 95% confidence interval? 2) What is the level of significance for a 95% confidence interval?...

STA2023-G3-5-07052021-215C David Gonzalez & | 07/18/21 8:52 PM Test: Week 2 Test (4.1-4.5, 5.1-5.3, 10.1-10.2) Time Remaining: 02:17:42 Submit Test This Question: 5 pts 15 of 20 (6 complete) This...