Refer to the subject-specific model (10.8) for binary matched pairs. 

a. Show that exp(β) is a conditional odds ratio between observation and outcome. Explain the distinction between it and the odds ratio exp(β) for model (10.6).

b. For a random sample of n pairs, explain why

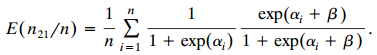
Similarily, state E(n₁₂/n). Using their ratio for fixed n and as n †’ ˆž, explain why

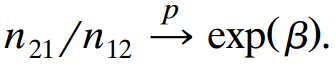
(Apply the law of large numbers due to A. A. Markov for independent but not identically distributed random variables, or use Chebyshev€™s inequality.)

c. Show that the Mantel€”Haenszel estimator (6.7) of a common odds ratio in the 2 × 2 × n form of the data simplifies to exp(β̂) = n₂₁/n₁₂.

exp(a; + B) 1 + exp(a; + B) ( /) 1 + exp(a;) i= i=1 exp(). 21