The Pearson residual for a cell in a two-way table equals ej (niji).

a. Show that they provide a decomposition of the Pearson chi-squared statistic, through X =

b. Show that Pearson residuals are smaller than adjusted residuals and thus have smaller variance than standard normal variates.

c. For 2 x 2 tables, show that (i) all four adjusted residuals have the same absolute value. (This is sensible, since df = 1 and the table contains only one piece of information about association.) Show that (ii) the four Pearson residuals may take different values; (iii) the square of each adjusted residual equals X2. (Note: For 2 x 2 tables, X² simplifies to

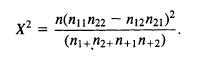
Adjusted residuals are identical for Poisson and binomial sampling. The Pearson residual defined here refers to Poisson sampling, and a different Pearson residual applies for binomial sampling; see Section 5.3.3.)

x n(1122-1221) (1+2+n+1+2)