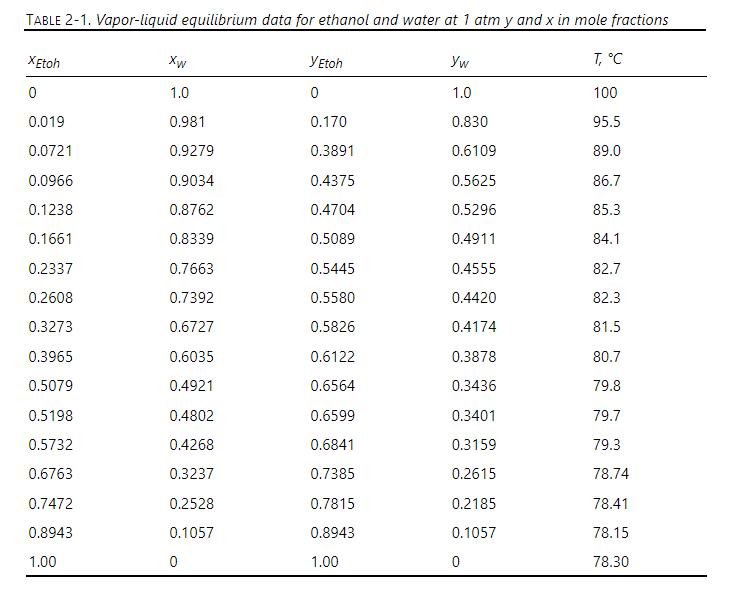
Errors in mass transfer coefficients obviously affect the value of \(\mathrm{H}_{\mathrm{G}}\) and hence the height of the packed section. These errors also affect calculation of \(\mathrm{y}_{\mathrm{AI}}\) and thus calculation of \(\mathrm{n}_{\mathrm{G}}\) and the height of the packed section. Return to the calculation in Example 16-1. We want to calculate the change in \(\mathrm{y}_{\mathrm{AI}}-\mathrm{y}_{\mathrm{A}}\) and in \(1 /\left(\mathrm{y}_{\mathrm{AI}}-\mathrm{y}_{\mathrm{A}}\right)\). We will do this calculation for a value of \(y_{A}=0.8\). Assume that the equilibrium values given in Table 2-1 follow a straight line between \(\mathrm{x}=0.7472\) and \(\mathrm{x}=\) 0.8943 , and determine the equation for this straight line.

Example 16-1

Table 2-1

a. Calculate the range of values of \(1 /\left(y_{\mathrm{AI}}-\mathrm{y}_{\mathrm{A}}\right)\) for a value of \(\mathrm{y}_{\mathrm{AI}}=\) 0.8 if \(\mathrm{H}_{\mathrm{G}}\) varies by \(\pm 24.4 \%\) compared to the \(0.4054 \mathrm{~m}\) used in Example \(16-1\), but \(\mathrm{H}_{\mathrm{L}}\) does not vary from the \(0.253-\mathrm{m}\) value. Then, assuming the percent of error in \(1.0 /\left(\mathrm{y}_{\mathrm{AI}}-\mathrm{y}_{\mathrm{A}}\right)\) is constant throughout the enriching section, estimate range in values of \(n_{G}\) and in height of packing (remember that \(\mathrm{H}_{\mathrm{G}}\) varies).

Example 16-1

b. Calculate the range of values of \(1 /\left(y_{A I}-y_{A}\right)\) for a value of \(y_{A}=\) 0.8 if both \(\mathrm{H}_{\mathrm{G}}\) and \(\mathrm{H}_{\mathrm{L}}\) vary by \(\pm 24.2 \%\) compared to \(0.4054 \mathrm{~m}\) and \(0.253 \mathrm{~m}\) used in Example 16-1 for \(\mathrm{H}_{\mathrm{G}}\) and \(\mathrm{H}_{\mathrm{L}}\), respectively. Then, assuming the percent of error in \(1.0 /\left(\mathrm{y}_{\mathrm{AI}}-\mathrm{y}_{\mathrm{A}}\right)\) is constant throughout the enriching section, estimate the range in values of \(\mathrm{n}_{\mathrm{G}}\) and in the height of packing (remember that \(\mathrm{H}_{\mathrm{G}}\) varies).

Example 16-1

Repeat Example 4-3 (distillation of ethanol and water) except using a column packed with 2.0- in. metal Pall rings. F = 1000.0 kmol/h, z = 0.20, Tp = 80.0F, xp = 0.80, xg = 0.02, L/D = 5/3, and p = 1.0 atm. Use a vapor flow rate that is nominally 75% of flooding. In the enriching section HG = 0.4054 m and H = 0.253 m, and in the stripping section HG = 0.2835 m and H = 0.1067 m (determined in Example 16-2). Example 4-3 A distillation column with a total condenser and a partial reboiler is separating an ethanol- water mixture. Feed is 20 mol% ethanol, feed rate is 1000 kmol/h, and feed temperature is 80F. Distillate is 80 mol% ethanol, and bottoms is 2 mol% ethanol. External reflux ratio is 5/3. Reflux is a saturated liquid, and CMO can be assumed. Pressure is 1 atm. Find optimum feed plate location as stages above the reboiler and total number of equilibrium stages. Example 16-2 Estimate values of HG and H for the distillation in Examples 4-3 and 16-1 using 2.0-in. metal Pall rings.