For the same system as in Problem 15.D1, the high concentration \(\mathrm{C}_{\mathrm{A}, 0}=1.2 \mathrm{~kg} / \mathrm{m}^{3}\) and \(\mathrm{C}_{\mathrm{A}, \mathrm{L}}=0.9701 \mathrm{~kg} / \mathrm{m}^{3}\), which is same as in Problem 15.D1, but we want a flux rate \(=0.35 \times 10^{-5} \mathrm{~kg} /\left(\mathrm{m}^{2} \mathrm{~s}\right)\). Apparatus temperature can be adjusted. Estimate the Fickian infinite dilution diffusivity by adjusting the value from Table 15-3 for the temperature difference by assuming that \(\mathrm{E}_{\mathrm{o}}=3000 \mathrm{cal} / \mathrm{mol}\) in Eq. \((15-22 \mathrm{c})\). What temperature is required?

Data From Problem 15.D2.

Repeat the numerical integration in Example 15-5, except use the quadrature formula, Eq. \((9-12)\)

Example 5-5

Equation (9-12)

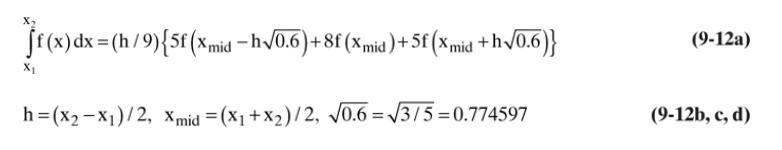
Table 15-3

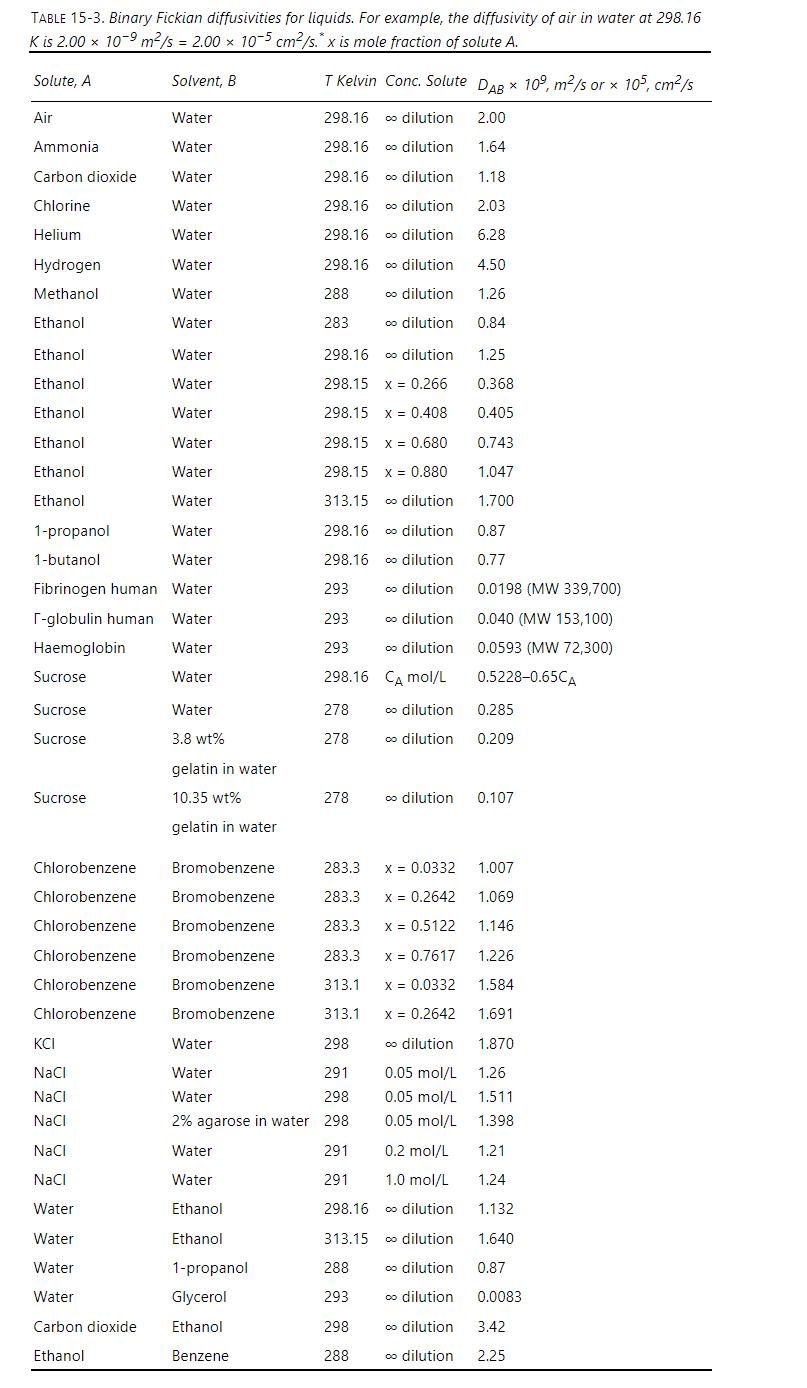
Equation (15-22c)

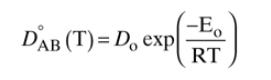
A steady-state system of ethanol and water has equimolar counterdiffusion across a liquid film of thickness 1.2 10-5m. At z = 0, the ethanol mole fraction is 0.010, and at z = L, the ethanol mole fraction is 0.300. Operation is at 40C. Find the flux of ethanol.