If the RANS equation (17.5) is subtracted from the unaveraged (mathrm{N}-mathrm{S}) equation (17.1), we obtain the following
Question:
If the RANS equation (17.5) is subtracted from the unaveraged \(\mathrm{N}-\mathrm{S}\) equation (17.1), we obtain the following equation for the perturbation velocity:
\[\begin{equation*}\frac{\partial v_{i}^{\prime}}{\partial t}+V_{j}\left(v_{i}^{\prime}, j\right)+v_{j}^{\prime}\left(V_{i}, j\right)+v_{j}^{\prime}\left(v_{i}^{\prime}, j\right)=-\left(p^{\prime} \delta_{i j} / ho\right)_{, j}+v\left(v_{i}^{\prime}\right)_{, j j}+\left\langle v_{i}^{\prime} v_{j}^{\prime}\rightangle_{, j} \tag{17.53}\end{equation*}\]
Verify this equation. Take the dot product of this equation with the perturbation velocity. From this equation derive an equation for the turbulent kinetic energy shown below:
\[\begin{equation*}\left.\frac{\partial k}{\partial t}+V_{j} \frac{\partial k}{\partial x_{j}}=\left\langle v_{i}^{\prime} v_{j}^{\prime}\rightangle \frac{\partial V_{i}}{\partial x_{j}}-\frac{\partial}{\partial x_{j}}\left\{v_{j}^{\prime}\left[p^{\prime} / ho\right]+k\right)\right\}+v\left\langle v_{i}^{\prime} abla^{2} v^{\prime}\rightangle \tag{17.54}\end{equation*}\]
The LHS has the standard form for convective transport with a mean velocity and represents the substantial derivative of the kinetic energy. The terms on the RHS are written as the divergence of a flux vector, a generation term, and a loss (dissipation) term. This provides the rationale for the engineering model for \(k\) given by Eq. (17.47).
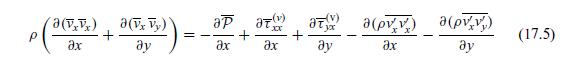
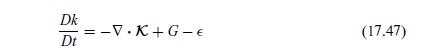
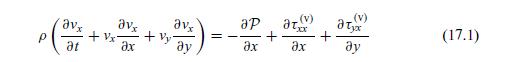
Step by Step Answer:

Advanced Transport Phenomena Analysis Modeling And Computations
ISBN: 9780521762618
1st Edition
Authors: P. A. Ramachandran





