Solve the non-linear equation for the double-layer potential given by [begin{equation*}abla^{2} phi=-frac{2 v F C_{infty}}{epsilon} sinh left[F u phi /left(R_{mathrm{G}} T ight) ight] tag{22.46}end{equation*}] Use

Solve the non-linear equation for the double-layer potential given by

\[\begin{equation*}abla^{2} \phi=-\frac{2 v F C_{\infty}}{\epsilon} \sinh \left[F u \phi /\left(R_{\mathrm{G}} T\right)\right] \tag{22.46}\end{equation*}\]

Use the dimensionless variables

\[\phi^{*}=\phi \frac{F v}{R_{\mathrm{G}} T}\]

and scale the distance by the Debye length. Show that the following dimensionless equation holds for the potential:

\[\frac{d^{2} \phi^{*}}{d x^{* 2}}=\sinh \left(\phi^{*}\right)\]

Solve the equation subject to the boundary condition that \(\phi^{*}=\phi_{\mathrm{s}}^{*}\) at \(x^{*}=0\) and is zero at \(x^{*} \rightarrow \infty\). Derive the following solution to the potential field:

\[\phi^{*}=2 \ln \left[\frac{1+\exp \left(-x^{*}\right) \tanh \left(\phi_{\mathrm{s}}^{*} / 4\right)}{1-\exp \left(-x^{*}\right) \tanh \left(\phi_{\mathrm{s}}^{*} / 4\right)}\right]\]

How does this compare with the linear model represented by Eq. (22.37)? What is the limit of the above expression for small values of the surface potential \(\phi_{\mathrm{s}}^{*}\) ?

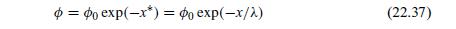
= exp(-x*) = x(-x/) (22.37)