Question: In 1545, a method of solving a cubic equation of the form x 3 + mx = n, developed by Niccolo Tartaglia, was published in

In 1545, a method of solving a cubic equation of the form x³ + mx = n, developed by Niccolo Tartaglia, was published in the Ars Magna, a work by Girolamo Cardano. The formula for finding the one real solution of the equation is

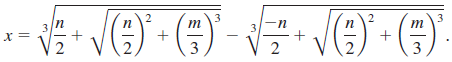
NO)-Ө)-O -Ө 3 )-(-) u. () 3п 3 3 х— Vz

x³ + 9x = 26

2 2 3 n n -n m + ()*+G) -+ G* +G) 3 3 x = 2 3 2 3 m 3

Step by Step Solution

★★★★★

3.36 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

e e e x For x39x26 m 9 and n1 26 Su... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related College Algebra Questions!

Create (either orally or in written form) a plan for how you will reach the desired profit goal. As you formulate your plan, remember that it costs money to make money. So, if your plan is to...

1545 Ocean Avenue LLC was formed for a real estate development. It was owned 50-50 by two other companies, Ocean Suffolk and Crown Royal, which each had a membership certificate in 1545. The...

A recent news release published by Ars Technica, LLD presented the results of a study concerning the world and domestic market share for the major manufacturers of personal computers (PCs). The file...

In finding eigenvalues by solving differential equations, quantization occurs only when we apply the condition that the eigenfunctions be well behaved. Ladder operators were used in Section 5.4 to...

In 1545, a method of solving a cubic equation of the form x 3 + mx = n, developed by Niccolo Tartaglia, was published in the Ars Magna, a work by Girolamo Cardano. The formula for finding the one...

Problem 9-5A Calculating depreciation-partial periods LO2, 3 West Coast Tours runs boat tours along the west coast of British Columbia. On March 5, 2020, it purchased, with cash, a cruising boat for...

Hi, I would like to download document from the AC556 budgeting project for Fantastic, Inc.: 6263003_ACC.xlsx I found the link from Google but I login and the document does not appear anymore for me...

On the 1040 form how do you calculate Ordinary dividends? Qualified dividends? Gain / loss? Rental estate, royalties? There are other boxes that I am confused on how to solve, but for now I need to...

(City_Precipitation_Data.txt). The data file contains the precipitation data for 66 US cities. Then proceed to write a java program. First, write four methods: 1 st method : Write a method that has...

a. je. Le- C. Additional transactions were as follows: Purchased equipment costing R 500,000. b. Sold equipment costing R600,000 with a book value of R250,000 for R400,000. Retired preferred stock at...

SportCo Inc are producing sports cars in the USA and are looking to expand their operations. They have analyzed their opportunities and are currently considering two potential ways to expand either...

The cost of equity of an unlevered firm (Note: cost of equity of unlevered firm = return on assets = cost of capital of the firm's assets = R A ) is 14.43%. Assume no taxes. ABC Company has a cost of...

Through the consolidated return rules, the IRS totally eliminates corporate taxpayers' ability to manage the combined tax liability of the members of the group. True False

Shared decision making is A. A provision of the Affordable Care Act B. Defined as a collaborative process that allows patients and their provider to make health decisions together C. Both A and B D....

Solve the quadratic equation. Check your answers. 49k + 4 = -28k

Solve the quadratic equation. Check your answers. 25k + 1 = 10k

Write the expression in standard form. 1 1 + i

Suppose that you own 2,800 shares of Nocash Corp. and the company is about to pay a 25% stock dividend. The stock currently sells at $125 per share. a. What will be the number of shares that you hold...

A company applies overhead using machine hours. Additional information follows. Standard variable overhead rate Actual variable overhead rate Standard hours of machine use ( for actual production )...

Reactive Power Generation has the following capital structure. Its corporate tax rate is 21%. Security Debt Preferred stock Common stock Market Value $ 10 million 30 million 60 million Required Rate...