FREE Trial

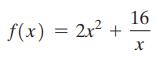
In Problems 750, follow Steps 1 through 7 on page 367 to graph each function. Steps for Graphing a Rational Function R STEP 1: Factor the numerator and denominator of R. Find the domain of the rational function. STEP 2:

In Problems 7–50, follow Steps 1 through 7 on page 367 to graph each function.


image


image

Transcribed Image Text:

Steps for Graphing a Rational Function R STEP 1: Factor the numerator and denominator of R. Find the domain of the rational function. STEP 2: Write R in lowest terms. STEP 3: Find and plot the intercepts of the graph. Use multiplicity to determine the behavior of the graph of R at each x-intercept. STEP 4: Find the vertical asymptotes. Graph each vertical asymptote using a dashed line. Determine the behavior of the graph of R on either side of each vertical asymptote. STEP 5: Find the horizontal or oblique asymptote, if one exists. Graph the asymptote using a dashed line. Find points, if any, where the graph of R intersects the asymptote. Plot the points. STEP 6: Use the real zeros of the numerator and denominator of R to divide the x-axis into intervals. Determine where the graph of R is above or below the x-axis by choosing a number in each interval and evaluating R. Plot the points found. STEP 7: Use the results obtained in Steps 1 through 6 to graph R.

This problem has been solved!


Do you need an answer to a question different from the above? Ask your question!
  • Tutor Answer

f x 2x Step 1 Domain x x 0 Step 4 16 2x 16 2 x 8 2 x 2 x 2x 4 x Step 5 X Step 6 …View the full answer


answer-question
Related Book For  answer-question
College Algebra

College Algebra

ISBN: 9780135226865

11th Edition

Authors: Michael Sullivan, Michael Sullivan III

See More Books
Question Details
Chapter # 5
Section: 5.4 Exercisess
Problem: 48
Posted Date: June 07, 2023 09:09:51
See More Questions

Students also viewed these Mathematics questions

Q:
In Problems 750, follow Steps 1 through 7 on page 367 to graph each function. Steps for Graphing a Rational Function R STEP 1: Factor the numerator and denominator of R. Find the domain of the...
A:
f x x Step 1 1 x 1 x 1 x x 1 X Step 4 Step 5 Step 6 x Step 2 3 f x Domain x x......
Q:
In Problems 750, follow Steps 1 through 7 on page 367 to graph each function. Steps for Graphing a Rational Function R STEP 1: Factor the numerator and denominator of R. Find the domain of the...
A:
9 2x 9 f x 2x Step 1 Step 4 Step 5 Step 2 3 f x Step 6 Domain x x 0 There is no y int......
Q:
In Problems 750, follow Steps 1 through 7 on page 367 to graph each function. Steps for Graphing a Rational Function R STEP 1: Factor the numerator and denominator of R. Find the domain of the...
A:
f x x Step 1 Step 4 1 x 1 Step 5 Step 6 X X Step 2 3 f x Domain x x 0 There is no y......
Q:
Use Theorem 3.11 to evaluate the following limits. THEOREM 3.11 Trigonometric Limits sin x lim X-0 X 1 lim x-0 COS X x = 0
A:
As given lim sin7x sin3x x0 Applying the tri......
Q:
Anpax, Inc., manufactures two products: L7 and Q2. Overhead is allocated to products based on machine hours. Management uses a flexible budget to forecast overhead. For the current year, fixed...
A:
a Overhead rate Expected number of machine hours L7 4 hours unit 25 000 units 100 000 hours Q2 5 hours unit 35 000 units 175 000 Budgeted denominator......
Q:
Paulson Corporation??s unadjusted trial balance at December 1, 2012, is presented below. The following transactions occurred during December.Dec. 2 Paulson purchased equipment for $16,000, plus sales...
A:
a Dec 2 Equipment 16 800 Cash 16 800 2 Depreciation Expense 450 Accumulated Depreciation Equipment 450 Cash 3 500 Accumulated Depreciation Equipment 2 250 Equipment 5 000 Gain on Disposal of Plant Ass......
Q:
If limits are imposed on medical-malpractice suits, then patients will not be adequately compensated for their injuries; but if the cost of malpractice insurance continues to rise, then physicians...
A:
Click to View...
Q:
Dane Cosmetics is evaluating a new fragrancemixing machine. The machine requires an initial investment of $24,000 and will generate after-tax cash inflows of $5,000 per year for 8 years. For each of...
A:
a 10 N 8 I 10 PMT 5000 Solve for PV 26 674 63 NPV PV n Initial investment NP......
Q:
Create an index.html page that will serve as your site home page, the home page should include the following: The driving school name must be in the header section. The driving school's name is Nsuku...
A:
I will provide an explanation of each part of the requested website structure and styling without including the actual code Homepage index html 1 Header Displays the driving school s name Nsuku Drivin......
Q:
In Problems 750, follow Steps 1 through 7 on page 367 to graph each function. Steps for Graphing a Rational Function R STEP 1: Factor the numerator and denominator of R. Find the domain of the...
A:
F x Step 1 x2x 15 x 6x 9 Step 4 Step 5 Step 6 x 5 x 3 x 5 x 3 x 3 x 3 Domain x x 3 The y intercept i......
Q:
In Problems 1954, solve each inequality algebraically. x + 4 x-2 1
A:
x 4 x 2 x 4 1 10 x 2 x 4 x 2 0 x 2 6 x 2 6 x......
Q:
The following misstatements are included in the inventory and related records of Westbox Manufacturing Company: 1. An inventory item was priced at $12 each instead of at the correct cost of $12 per...
A:
MISSTATEMENT a CONTROL THAT SHOULD HAVE PREVENTED THE MISSTATEMENT FROM OCCURRING Internal verificat......
Q:
1. The following data give the 2007 gross domestic product (GDP) in billions of dollars for all 50 states. The data are entered in alphabetic order by state (Bureau of Economic Analysis, June 2005)....
A:
a To calculate the mean and median for the given data you can follow these steps Calculate the Mean Sample Statistic The mean also known as the averag......
Q:
Analyze the wisdom of Solomon found in the verses from the book of Proverbs 1:1 and 9:18 for this week. How do these verses apply to modern marketing? What concerns do they address regarding the...
A:
The Book of Proverbs in the Bible contains wisdom literature and while it may not directly address modern marketing practices its principles can be ap......
Q:
You want to buy a house that currently costs $350.000. The bank requires 22%down and 12-year mortgage rates are around 4.02%. Ignoring other costs and expenses associated with the house, what would...
A:
To calculate the quarterly mortgage payments for a house costing 350 000 with a 12 year mortgage and......
Q:
(a). The radius of a cylinder increases at the rate of 0.4 cm/s while the heght decreases at the rate of o.8 cm/s. Find the rate at which the volume is changing at the instant when r 7cm and h-14cm....
A:
a To find the rate at which the volume of the cylinder is changing at the given instant we can use t......
Q:
(a) Peter owned a 5-year bond A with a coupon rate of 6.6% p.a., paying coupon semi-annually and with a face value of $1,000. The bond is callable in 2 years with a call price of $1,080. If the yield...
A:
a Bond Price with Callable Feature Given data Coupon rate 6 6 per annum Coupons paid semi annually Face value 1 000 Callable in 2 years at 1 080 Yield......
Q:
During the month of March, QNI Corporation made the following credit sales and had the Following related collections. QNI prepares financial statements for the first quarter of operations at the end...
A:
a 3 3 Accounts Receivable A 1 400 Sales R SE 1 400 Made sale on account 3 8 Accounts......
Q:
Recall that Chapter 8 described the binary search algorithm for finding a particular entry in an ordered list. The idea behind binary search is to begin looking in the exact center of the list. If...
A:
32 6 halvings 64 7 h......
Q:
Balance this four-column account. What function does the PR column serve? When will Account 111 be used in the journalizing and posting process? Cash Acct. 111 Balance Dr. Cr. Date Explanation PR Dr....
A:
Cash 111 Balance Date PR Dr Cr Dr Cr 201X Mar 6 GJ1 29 29 10 G......
Q:
Balance this four-column account. What function does the PR column serve? When will Account 111 be used in the journalizing and postingprocess? Cash Acct. 111 Balance Date 201X Explanation PR Dr....
A:
cash 111 balance 201X date exp ref dr cr dr cr Nov 7 gj1 70 7......
Q:
Transactions related to revenue and cash receipts completed by Aspen Architects Co. during the period June 230, 2012, are as follows: June 2. Issued Invoice No. 793 to Nickle Co., $4,900. 5. Received...
A:
1 and 5 GENERAL LEDGER Cash 11 Post Balance Date Item Ref Dr Cr Dr Cr 2012 June 1 Balance 11 350 30......
Q:
In Problems 1130, solve each equation by factoring. x 2 - 9x = 0
A:
x 9x 0 x x 9......
Q:
The bullish sentiment of individual investors was 27.6% (AAII Journal, February 2009). The bullish sentiment was reported to be 48.7% one week earlier and 39.7% one month earlier. The sentiment...
A:
One week earlier One month earlier a Point estimate......
Q:
A sports psychologist studied the effect of a motivational program on injuries among players of three different sports. The following chart shows the design. For each of the following possible...
A:
Condition Condition Condition a With motivational program Wi......
Q:
A written preliminary contractual instrument prepared prior to the issuance of a definitive contract that authorizes the contractor to begin work immediately, within certain limitations, is known as...
A:
C Lett......
Q:
The executive team at Current Designs has gathered to evaluate the companys operations for the last month. One of the topics on the agenda is the special order from Huegel Hollow, which was presented...
A:
a Quantity variance for polyethylene powder Unfavorable Price variance for polyethylene powder Unfav......
Q:
Please pick a side. Do you see the era of womens protective labor legislation as a positive or negative when it comes to advancing womens position in paid employment? Whichever position you took in...
A:
Position The Era of Women s Protective Labor Legislation as a Positive for Advancing Women s Position in Paid Employment 1 Persuasive Arguments Early......
Q:
A friend of yours sent an e-mail asking about generally accepted accounting principles ( GAAP ). It seems your friend was browsing through Whirlpool Corporations recent annual report and she spotted...
A:
Requirement 1 What are generally accepted accounting principles GAAP GAAP refers to the network of conventions rules guidelines and procedures that shape the financial reporting practices of businesse......
Q:
Provide the explanation for each of these general journal entries. GENERAL JOURNAL Page 4 Date Account Titles and Descriptions PRI Debit Credit 2012 June 11 Cash 1700000 2600 000 Office Equipment B....
A:
A Owner s investment o......
Q:
The following trial balance was prepared incorrectly. Lee Company Trial Balance October 31, 2014 a. Rearrange the accounts in proper order. b. Calculate the total of the trial balance. (Small numbers...
A:
LEE COMPANY TRIAL BALANCE OCTOBER 31 2014......
Q:
In Exercises evaluate the definite integral. TT/2 J-T/2 3 cos x dx
A:
2 2723 cos x d......
Q:
A company makes consumer products. Revenues have been growing at 2% a year very steadily. The company has been very conservative with its business approach. It has been happy to just maintain market...
A:
Creditworthiness and performance evaluation of CEOs depend on various factors and the transition fro......
Q:
What are the underlying causes of the opioid crisis, including factors related to prescription practices, illicit drug markets, and social determinants of health? 2. How does the opioid crisis impact...
A:
1 The underlying causes of the opioid crisis can be attributed to a variety of factors including prescription practices illicit drug markets and social determinants of health Regarding prescription pr......
Q:
The expected market risk premium is 10%. TGT common stock has a beta of 1.05. The U.S. Treasury bill ( rf) is yielding 2.0% and TGT's tax rate is 25%. What is JACK's cost of equity capital?
A:
To calculate JACK s cost of equity capital we need to use the......
Q:
Ritu has been working as HR Head for Company ABC, a Indian-based manufacturing firm with global presence, for over 30 years. ABC has a long-standing reputation as a company that stands by its core...
A:
Q1 What aspects of Emotional Intelligence are not being used in this situation by Ram Ritu or Shyam Emotional Intelligence EI involves understanding and managing emotions in oneself and others In this......
Q:
Think about a time when you experienced a cultural collision as a result of miscommunication (or another example that you are aware of). How did the different cultures (people) attempt communicate...
A:
I don t have personal experiences or emotions but I can certainly share an example of a cultural col......
Q:
Determine whether the statement is always true, sometimes true, or never true. Explain your answer. Two lines that are both parallel to a third line must be parallel to each other.
A:
Always true If any......
Q:
Splitting hairs, if you shine a beam of colored light to a friend above in a high tower, will the color of light your friend receives be the same color you send? Explain.
A:
To conclude I can say that the photons of light a......
Q:
Crandell Co. forecasts monthly production of 20,000 units at a cost of $20 each. The cost breakdown is as follows: Labor...............2 hours per unit at $4 per hour Material............3 pounds per...
A:
Computation of the following Direct labo......
Q:
The beginning inventory was 300 units at a cost of $10 per unit. Goods available for sale during the year were 1,300 units at a total cost of $14,400. In May, 600 units were purchased at a total cost...
A:
a Beginning inventory 300 units 10 per unit May purchases......
Q:
The beginning inventory was 900 units at a cost of $10 per unit. Goods available for sale during the year were 3,900 units at a total cost of $43,200. In May, 1,800 units were purchased at a total...
A:
a Beginning inventory 900 units 10 per unit May purchases 1 800 units per unit 19 800 October purcha......
Q:
Implement a generic Map that supports the put and get operations. The implementation will store a hash table of pairs (key, definition). Figure 5.55 provides the Map specification (minus some...
A:
public class Map KeyType ValueType public Map items new QuadraticProbingHashTable public void put Ke......
Q:
Why is finding financial assistance for international expansion more difficult than finding such help for domestic expansion?
A:
Many financial sources do not like the time it takes to......
Q:
Your airplane crashes in the Pacific Ocean. You land on a desert island with one other passenger. A box containing 100 little bags of peanuts also washes up on the island. The peanuts are the only...
A:
In this case the Edgeworth Box is actually a line because there is only one good on the island The set of possible allocations is a straight line 100 units long Every allocation is Pareto efficient.........
Q:
If high school clinics are to stem the tide of teenage pregnancy, then they must dispense birth-control devices; but if they want to discourage illicit sex, then they must not dispense these devices....
A:
Click to View...
Q:
Dominique Fouque owns and operates Dominique's Doll House. She has a small shop in which she sells new and antique dolls. She is particularly well known for her collection of antique Ken and Barbie...
A:
1 2 3 4 5 Should the adjustment be reversed a Never reverse adjustments for merchandise invent......
Q:
What is the difference between a product and a brand? Do you think Apples's success is just thanks to a top of the line well functioning product or branding had a role in it?
A:
The difference between a product and a brand lies in their fundamental characteristics and how they are perceived by consumers 1 Product A product is......
Q:
Josephine Mater works for the supply-chain analytics division of Trader Joes, a national chain of specialty grocery stores. Trader Joes is considering a redesign of its supply chain. Josephine knows...
A:
The solution for eight clusters is shown below According to this solution between one Clusters 4 and......
Q:
The Vallejo Company expects purchases for 2016 to be $160,000 in the first quarter, $240,000 in the second quarter, $190,000 in the third quarter, and $300,000 in the last quarter. All purchases are...
A:
Computation of the following Particulars......
Q:
The Vallejo Company expects purchases for 2016 to be $160,000 in the first quarter, $240,000 in the second quarter, $190,000 in the third quarter, and $300,000 in the last quarter. All purchases are...
A:
Computation of the following Particulars......
Q:
Computer forensics and data recovery refer to the same activities. True or False?
A:
Computer forensics involves the digital evidence in support of cri......
Q:
Several hundred PCs are in use at the corporate headquarters for National Insurance Corporation. The pattern of breakdowns for these PCs follows a Poisson distribution with an average rate of 4.5...
A:
Let s break down each part of this problem step by step a The average time required to repair a PC is given as 1 day Since there are 5 working days in......
Q:
Water at 20C flows in a partially full 3-m-diameter circular channel at an average velocity of 2 m/s. If the maximum water depth is 0.75 m, determine the hydraulic radius, the Reynolds number, and...
A:
To determine the hydraulic radius Reynolds number and flow regime you can follow these steps Calcula......
Q:
A researcher is comparing patients with high medication compliance versus those with low medication compliance in an outpatient psychiatric day program utilizing the Hamilton Anxiety Rating Scale...
A:
The median of a normal distribution is the same as the mean s......
Q:
Construct a series of four terms that exhibits increasing intension but nondecreasing extension.
A:
In logic and philosophy intension and extension refer to the concepts of the scope or meaning of a t......
Q:
Go to http://analytics-magazine.org/issues/digitaleditions, and find the January/February 2013 edition titled Work Social. Read the article Big Data, Analytics and Elections, and answer the following...
A:
a In general Big Data in the context of elections could include voter registration data polling data......
Q:
You are the Director of Adult Prisons for the State of Ohio. Gangs have negatively impacted many of your maximum security institutions, and violence has escalated. You would like to move all known...
A:
1 Planning for Change In order to effectively implement the consolidation of known gang members into one unit at a single institution while also addressing the various challenges presented I would fol......
Q:
Use translations to graph f. f(x) = x-/2 +1
A:
1 2 1 2 Shift the graph......
Business And Professional Communication KEYS For Workplace Excellence 4th Edition - ISBN: 1506369596 - Free Book