Each round in a block cipher should be invertible to make the whole block invertible. Modern block ciphers use two approaches to achieve this. In the first approach, each component is invertible; in the second approach some components are not invertible but the whole round is invertible using what is called a Feistel cipher. This approach is used in DES, described in the text. The trick in the Feistel cipher is to use the XOR operation as one of the components. To see the point, assume that a round is made of a noninvertible component, NI, and an XOR operation, as shown in Figure 31.29. Prove that the whole round is invertible, which means that the plaintext can be recovered from the ciphertext. 

Figure 31.29

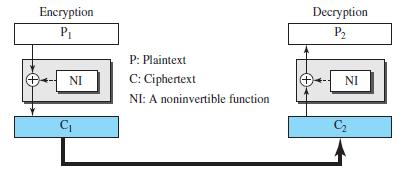
Encryption Decryption Pi P: Plaintext C: Ciphertext NI NI NI: A noninvertible function C