Repeat 7.6.1, assuming that updates to C incur a cache miss due to false sharing when consecutive elements are in a row (i.e., index i) are updated.

Exercise 7.6.1

Assume that we are going to compute C on both a single core shared memory machine and a 4-core shared-memory machine. Compute the
speedup we would expect to obtain on the 4-core machine, ignoring any memory issues.

Matrix multiplication plays an important role in a number of applications. Two matrices can only be multiplied if the number of columns of the first matrix is equal to the number of rows in the second.

Let’s assume we have an m × n matrix A and we want to multiply it by an n × p matrix B. We can express their product as an m × p matrix denoted by AB (or A · B). If we assign C = AB, and c_i,j denotes the entry in C at position (i, j), then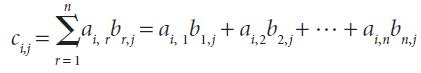

for each element i and j with 1 ≤  i m and 1 ≤ j p. Now we want to see if we can parallelize the computation of C. Assume that matrices are laid out in memory sequentially as follows: a_1,1, a_2,1, a_3,1, a_4,1, …, etc..

ij = W Tab=abyta r=1 i, 1,2 2,j ... ta b inni,j