Consider the following function for computing the product of an array of n double-precision numbers. We have unrolled the loop by a factor of 3.

For the line labeled “Product computation,” we can use parentheses to create five different associations of the computation, as follows:

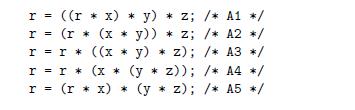
Assume we run these functions on a machine where floating-point multiplication has a latency of 5 clock cycles. Determine the lower bound on the CPE set by the data dependencies of the multiplication.

double aprod (double a[1, long n) { } long 1; double x, y, z; double r = 1; for (i =0; i < n-2; i+= 3) { X = a[i]; y = a[i+1]; z = a[i+2]; r = r * x * y* z; /* Product computation */ } for (i