The closed-loop system shown below is subjected to a disturbance \(\mathrm{N}(\mathrm{s})\). The transfer function \(\mathrm{C}(s) / \mathrm{N}(s)\) is given by

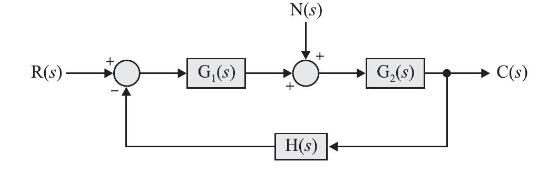
(a) \(\frac{\mathrm{G}_{1}(s) \mathrm{G}_{2}(s)}{1+\mathrm{G}_{1}(s) \mathrm{G}_{2}(s) \mathrm{H}(s)}\)
(b) \(\frac{\mathrm{G}_{1}(s)}{1+\mathrm{G}_{1}(s) \mathrm{H}(s)}\)
(c) \(\frac{\mathrm{G}_{2}(s)}{1+\mathrm{G}_{2}(s) \mathrm{H}(s)}\)
(d) \(\frac{\mathrm{G}_{2}(s)}{1+\mathrm{G}_{1}(s) \mathrm{G}_{2}(s) \mathrm{H}(s)}\)

R(s). G(s) N(s) H(s) G(s) C(s)