Question: The transfer function of the system shown below is (a) (frac{mathrm{Q}}{mathrm{R}}=frac{mathrm{ABC}}{1+mathrm{ABC}}) (b) (frac{mathrm{Q}}{mathrm{R}}=frac{mathrm{A}+mathrm{B}+mathrm{C}}{1+mathrm{AB}+mathrm{AC}}) (c) (frac{mathrm{Q}}{mathrm{R}}=frac{mathrm{AB}+mathrm{AC}}{mathrm{ABC}}) (d) (frac{mathrm{Q}}{mathrm{R}}=frac{mathrm{AB}+mathrm{AC}}{1+mathrm{AB}+mathrm{AC}}) R- + B Q

The transfer function of the system shown below is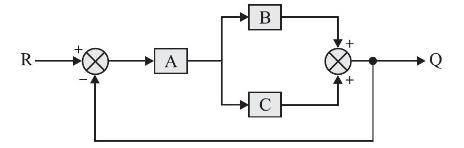 R- + B Q

(a) $\frac{\mathrm{Q}}{\mathrm{R}}=\frac{\mathrm{ABC}}{1+\mathrm{ABC}}$
(b) $\frac{\mathrm{Q}}{\mathrm{R}}=\frac{\mathrm{A}+\mathrm{B}+\mathrm{C}}{1+\mathrm{AB}+\mathrm{AC}}$
(c) $\frac{\mathrm{Q}}{\mathrm{R}}=\frac{\mathrm{AB}+\mathrm{AC}}{\mathrm{ABC}}$
(d) $\frac{\mathrm{Q}}{\mathrm{R}}=\frac{\mathrm{AB}+\mathrm{AC}}{1+\mathrm{AB}+\mathrm{AC}}$

R- + B Q

Step by Step Solution

★★★★★

3.32 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The image shows a block diagram of a system with three blocks labeled A B and C whose transfer funct... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Systems Analysis And Design Questions!

XZ Limited was formed on 1 August 201. Which items may appear in the statement of changes in equity for the year ended 31 July 202? Debenture Transfer to Ordinary share dividend paid Ordinary...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Question 3 Sample Sample Sample Sample Sample ATTRIBUTE NAME Data Data Data Data Data CUSTOMER_ID 100 100 125 CUSTOMER_NAME CUSTOMER_ADDRESS DINNER_ID Jenny Smith Jenny 34 Rose Street Smith 34 Rose...

Q 1 : Obtain the transfer function E o s E i ( s ) of the operational - amplifier circuit shown. Q 2 : Determine the transfer function x 2 s F ( s ) for the mechanical system shown knowing that M = 1...

This is a desktop based activity focussing on deriving the characteristic equation of DC motor followed by obtaining the behaviour of system in time and frequency domains using computer simulation...

(a) (b) (c) (d) Determine the open-loop transfer function for the system shown in Figure Q2 and hence obtain an expression for the closed-loop transfer function. [4] kas C + s+1 S +5 +1 Figure Q2...

answers WRONG? 3. In the following statements about an ideal operational amplifier, which one is A) It has very low input impedance, and very high gain; B) It has very high input impedance, and very...

(b) A sampler and a zero-order hold element were inserted into the system in Figure Ql(a) as shown in Figure Q1(b). Obtain the closed-loop pulse transfer function of this system and by using MATLAB...

In a system where the liquid level is controlled, the system's inlet is shown by R(s) and its output by C(s). R(s) C(s) Ge(s) G(s) The transfer function of the system has been subtracted as G(s)....

6) A continuous time plant with transfer function is to be included in the control system of Figure 1, with D(z) = K and T = 0.1s: system a) Find the open loop discrete transfer function of the b)...

A certain type of tomato seed germinates 90% of the time. A backyard farmer planted 25 seed. (Note: In the place of "HH" write last two digits of your registration number) (a) What is the probability...

1. Discuss why an entrepreneur might become overly committed to the entrepreneurs business, to the point of intentionally engaging in an illegal activity. 2. What philosophical principles did Chris...

When determining the number of days a taxpayer has rented a home during the year, a day for which a taxpayer rents a home to a non - relative for less than fair market value counts as a day of _ _ _...

Selecting managers for expatriate assignments means screening them for traits that predict success in adapting to dramatically new environments. Such traits include both "stable" and "dynamic"...

In Figure 10.22, assume we have 100 packets. We have created two sets of packets with high and low resolutions. Each high-resolution packet carries on average 700 bits. Each low-resolution packet...

Using the ideas in the previous two problems, we can create a general formula for correcting any number of errors (m) in a codeword of size (n). Develop such a formula. Use the combination of n...

Assume we want to send a dataword of two bits using FEC based on the Hamming distance. Show how the following list of datawords/codewords can automatically correct up to a one-bit error in...

Minden Company introduced a new product last year for which it is trying to find an optimal selling price. Marketing studies suggest that the company can increase sales by 5,000 units for each $2...

Consumers markets include schools households governments companies retailers

Create a Java EE application (A) Create a Java EE application with at least 3 web pages (B) Add all the features we learned in this course, including, JSP, JDBC, servlet, JAVA beans, mail, secure...