Problem 22 in Chapter 3 introduced the model for patients treated under a regimen of a single day of Glargine insulin (Tarn, 2005). The model

Problem 22 in Chapter 3 introduced the model for patients treated under a regimen of a single day of Glargine insulin (Tarín, 2005). The model to find the response for a specific patient to medication can be expressed in phase-variable form with

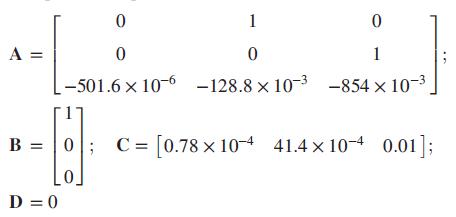
The state variables will take on a different significance in this expression, but the input and the output remain the same. Recall that u = external insulin flow, and y = plasma insulin concentration.

a. Obtain a state-feedback gain matrix so that the closed-loop system will have two of its poles placed at -1/15 and the third pole at -1/2.

b. Use MATLAB to verify that the poles appear at the positions specified in Part a.

Data from Problem 22

In the past, Type-1 diabetes patients had to inject themselves with insulin three to four times a day. New delayed-action insulin analogues such as insulin Glargine require a single daily dose. A similar procedure to the one described in the Pharmaceutical Drug Absorption case study of this chapter is used to find a model for the concentration-time evolution of plasma for insulin Glargine. For a specific patient, state-space model matrices are given by (Tarín, 2007)

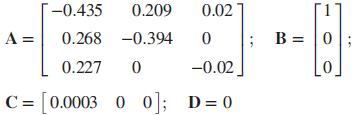
1 A = 1 -501.6 x 10-6 -128.8 x 10-3 -854 x 10-3 B = 0 C = [0.78 x 10-4 41.4 x 10-4 0.01]; %3D [o D = 0