Problem 23 in Chapter 1 discusses the cruise control of serial, parallel, and split-power hybrid electric vehicles (HEVs). The functional block diagrams developed for these HEVs indicated that the speed of a vehicle depends upon the balance between the motive forces (developed by the gasoline engine and/or the electric motor) and running resistive forces. The resistive forces include the aerodynamic drag, rolling resistance, and climbing resistance. Figure P2.40 illustrates the running resistances for a car moving uphill (Bosch, 2007).

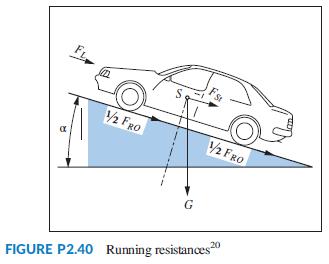
The total running resistance, Fw, is calculated as F_w = F_Ro + F_L + F_St, where F_Ro is the rolling resistance, F_L is the aerodynamic drag, and F_St is the climbing resistance. The aerodynamic drag is proportional to the square of the sum of car velocity, v, and the head-wind velocity, v_hw, or v + v_hw. The other two resistances are functions of car weight, G, and the gradient of the road (given by the gradient angle, α), as seen from the following equations:

F_Ro = fG cos α = fmg cos α

where

f = coefficient of rolling resistance

m = car mass; in kg

g = gravitational acceleration; in m/s²

F_L = 0:5ρC_wA(v + v_hw)².

and

ρ = air density; in kg/m³

C_w = coefficient of aerodynamic drag

A = largest cross-section of the car; in kg=m²

F_St = G sin α = mg sin α:

The motive force, F, available at the drive wheels is:

where

T = motive torque

P = motive power

i_tot = total transmission ratio

r = tire radius

η_tot = total drive-train efficiency:

The surplus force, F - Fw, accelerates the vehicle (or retards it when F_w > F). Letting a = F - Fw/km · m, where a is the acceleration and km is a coefficient that compensates for the apparent increase in vehicle mass due to rotating masses (wheels, flywheel, crankshaft, etc.):

a. Show that car acceleration,21 a, may be determined from the equation:
F = fmg cos α + mg sin α + 0:5ρC_wA(v + v_hw)² + km ma

b. Assuming constant acceleration and using the average value for speed, find the average motive force, F_av (in N), and power, P_av (in kW) the car needs to accelerate from 40 to 60 km/h in 4 seconds on a level
road, (α = 0°), under windless conditions, where v_hw = 0. You are given the following parameters: m = 1590 kg, A = 2m², f = 0:011, ρ = 1.2 kg/m³, C_w = 0.3, η_tot = 0.9; k_m = 1:2. Furthermore, calculate the additional power, P_add, the car needs after reaching 60 km/h to maintain its speed while climbing a hill with a gradient α = 5°.

c. The equation derived in Part a describes the nonlinear car motion dynamics where F (t) is the input to the system, and v(t) the resulting output. Given that the aerodynamic drag is proportional to v² under windless conditions, linearize the resulting equation of motion around an average speed, v_o = 50 km/h, when the car travels on a level road,22 where α = 0°. (Expand v² - v₀² in a truncated Taylor series). Write that equation of motion and represent it with a block diagram in which the block G_v represents the vehicle dynamics. The output of that block is the car speed, v(t), and the input is the excess motive force, F_e(t), defined as: F_e = F - F_St - F_Ro + F_o, where F_o is the constant component of the linearized aerodynamic drag.

d. Use the equation in Part c to find the vehicle transfer function: Gv(s) = V(s)/Fe(s).

Transcribed Image Text:

2 FRo 2 FRO α G 20 FIGURE P2.40 Running resistances