Bicksler Enterprises is considering a $10 million project that will last five years, with straight-line depreciation of $2 million per year. The cash revenues less cash expenses per year are $3.5 million. The corporate tax rate is 21 percent. The risk-free rate is 10 percent and the unlevered cost of equity is 20 percent.

The cash flow projections each year are:

Because the APV of a project is the sum of its all-equity value plus the additional effects of debt, we will examine each in turn.

All-Equity Value Assuming the project is financed with all equity, the value of the project is:

Initial cost + Depreciation tax shield + Present value of ( Cash revenues − Cash expenses )

This calculation uses the techniques presented in the early chapters of this book. Notice that we have assumed that the depreciation tax shield is risk free, and therefore discounted it at the riskless rate of 10 percent. If the firm believes the depreciation tax shield is risky, it can use a higher discount rate to reflect the riskiness of the depreciation tax shield.7 The revenues less expenses are discounted at the higher rate of 20 percent.

An all-equity firm would clearly reject this project because the NPV is −$138,827. And equity flotation costs would only make the NPV more negative. However, debt financing may add enough value to the project to justify acceptance. We consider the effects of debt next.

Additional Effects of Debt Bicksler Enterprises can obtain a five-year, nonamortizing loan for $7,500,000 after flotation costs at the risk-free rate of 10 percent. Flotation costs are fees paid when stock or debt is issued. These fees may go to printers, lawyers, and investment bankers, among others. Bicksler Enterprises is informed that flotation costs will be 1 percent of the gross proceeds of its loan. The previous chapter indicates that debt financing alters the NPV of a typical project. We look at the effects of debt next.

Flotation Costs Given that flotation costs are 1 percent of the gross proceeds, we have:

$7,500,000 = ( 1 − .01 ) × Gross proceeds = .99 × Gross proceeds The gross proceeds are: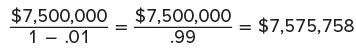

The flotation costs will be $75,758 ( = .01 × $7,575,758 ) . To check the calculation, note that net proceeds are $7,500,000 ( = $7,575,758 − 75,758 ) . In other words, Bicksler Enterprises receives only $7.5 million. The flotation costs of $75,758 are received by intermediaries such as investment bankers.

Flotation costs are paid immediately but are deducted from taxes by amortizing on a straight-line basis over the life of the loan. The cash flows from flotation costs are calculated as: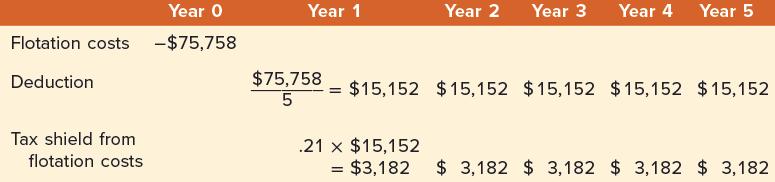

The relevant cash flows from flotation costs are in bold. When we discount at 10 percent, the tax shield has a net present value of:

The net cost of flotation is:

The net present value of the project after the flotation costs of debt but before the benefits of debt is:

Tax Subsidy Interest must be paid on the gross proceeds of the loan, even though intermediaries receive the flotation costs. Because the gross proceeds of the loan are $7,575,758, annual interest is $757,576 ( = $7,575,758 × .10 ) . The interest cost after taxes is $598,485 [ = $757,576 × ( 1 − .21 ) ] . Because the loan is nonamortizing, the entire debt of $7,575,758 is repaid at Year 5. These terms are indicated here:

The relevant cash flows are listed in the preceding table. They are (1) loan received, (2) annual interest cost after taxes, and (3) repayment of debt. Note that we include the gross proceeds of the loan as an inflow because the flotation costs have previously been subtracted.

In Chapter 16, we mentioned that the financing decision can be evaluated in terms of net present value. The net present value of the loan is the sum of the net present values of each of the three cash flows. This can be represented as follows:

Though we previously saw that an all-equity firm would reject the project, a firm would accept the project if a $7.5 million (net) loan could be obtained.

Because the loan discussed was at the market rate of 10 percent, we have considered only two of the three additional effects of debt (flotation costs and tax subsidy) so far. We now examine another loan where the third effect arises. A number of companies are fortunate enough to obtain subsidized financing from a governmental authority. Suppose that the project of Bicksler Enterprises is deemed socially beneficial and the state of New Jersey grants the firm a $7.5 million loan at 8 percent interest. In addition, all flotation costs are absorbed by the state. Clearly, the company will choose this loan over the one we previously calculated. The cash flows from the loan under the subsidized terms are calculated as: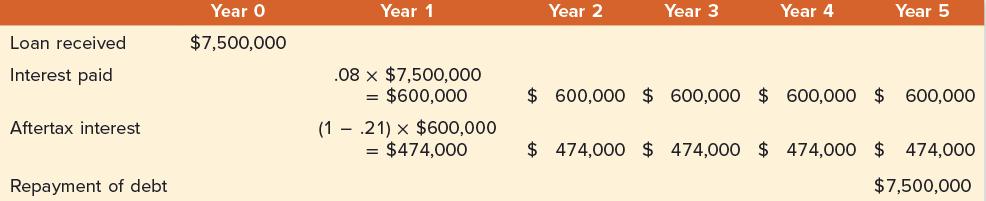

The relevant cash flows are listed in the preceding table. Using Equation 18.1, the NPV of the loan is:

Why do we discount the cash flows in Equation 18.1″ at 10 percent when the firm is borrowing at 8 percent? We discount at 10 percent because that is the fair, or market, rate.

That is, 10 percent is the rate at which the firm could borrow without benefit of subsidization.

The net present value of the subsidized loan is larger than the net present value of the earlier loan because the firm is now borrowing at the below-market rate of 8 percent. Note that the NPV of the loan calculation in Equation 18.1″ captures both the tax effect and the nonmarket rate effect.

The net present value of the project with subsidized debt financing is:

Transcribed Image Text:

Initial outlay Depreciation tax shield Revenue less expenses Year O -$10,000,000 Year 1 .21 x $2,000,000 = $420,000 (121) × $3,500,000 = $2,765,000 Year 2 Year 3 $ 420,000 $ 420,000 Year 4 $ 420,000 Year 5 $ 420,000 $2,765,000 $2,765,000 $2,765,000 $2,765,000