In streaming data classification, there is an infinite sequence of the form \((\mathbf{x}, y)\). The goal is to find a function \(y=f(\mathbf{x})\) that can predict the label \(y\) for an unseen instance \(\mathbf{x}\). Due to evolving nature of streaming data, the data set size is not known. In this problem, we assume \(\mathbf{x} \in[-1,1] \times\) \([-1,1]\) and \(y \in\{-1,1\}\), and the first eight training samples are shown below.

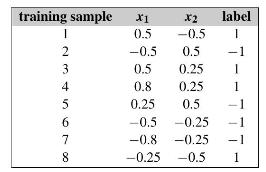
a. Suppose we have stored the first eight training samples. Now a test data point \(\mathbf{x}_{\text {test }}=\) \((0.7,0.25)^{T}\) comes. Use the \(k\)-nearest neighbors algorithm \((k-\mathrm{NN})\) to predict the label of \(\mathbf{x}_{\text {test }}\). You can set \(k=1\).
b. Due to the unknown size of streaming data, it could be infeasible to store all the training samples. However, if we divide the feature space into several subareas (e.g., \(A_{1}=\) \([0,1] \times[0,1], A_{2}=[-1,0) \times[0,1], A_{3}=[-1,0) \times[-1,0)\) and \(\left.A_{4}=[0,1] \times[-1,0)ight)\), it is efficient to store and update the number of positiveegative training samples in a subarea. Based on this intuition, devise an algorithm to classify stream data. What is the prediction of your algorithm on the test point \(\mathbf{x}_{\text {test }}=(0.7,0.25)^{T}\) given the first eight training samples?
c. Give an example on which the \(k\)-NN algorithm and your algorithm give different predictions. To let your algorithm mimic the idea of \(k-\mathrm{NN}\), how to improve it given a sufficient number of training data?

Transcribed Image Text:

training sample X1 0.5 -0.5 I 2 3 4 4561 6 7 8 label 1 X2 -0.5 0.5 0.5 0.25 0.8 0.25 0.25 0.5 -0.5 -0.25 -0.8 -0.25 -0.25 -0.5 1 1 I 1 T