(Correlation) Correlation is equivalent to covariance, except that correlations are normalized covari- ances. Correlation coefficients are frequently denoted by the Greek letter . If Var[z]

(Correlation) Correlation is equivalent to covariance, except that correlations are normalized covari-

ances. Correlation coefficients are frequently denoted by the Greek letter ρ. If Var[z] = [σ_ij] then the correlation between z_i and z_j is

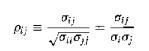
where standard deviations are σ_i = $\sqrt{\sigma_{ii}}$.

(a) Show that |ρ_ij| ≤ 1. [HINT: Consider the Cauchy-Schwarz inequality (Lemma 7.8).]

(b) Show that the MMSE linear predictor of z_i using z_j is given by

Interpret the terms in this expression.

(c) The partial correlation coefficient between z_i and z_j given z_k is defined to be the correlation coefficient between the residuals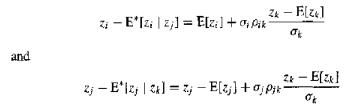
Find this partial correlation coefficient in terms of the correlation coefficients ρ_ij, ρ_ik, and ρ_jk and the standard deviations σ_i, σ_j, and σ_k.

Pij = ij