(LMLE) Suppose that the third derivatives of the log-likelihood function satisfy the uniform LLN

(Lemma 15.1, p. 321) so that

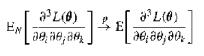
uniformly in $\theta \in \Theta$. Show that the initial consistent estimator in the LMLE can be merely $N^{-1/2}$-consistent for $\delta > \frac{1}{2}$, that is $N^{1/2}(\hat{\theta}_1 - \theta_0) = O_p(1)$.

aL(0) EN L(0) 2680,20