(Reparameterization) Example 16.9 notes that transforming the variance parameter in the log-likelihood function of the normal distribution improves the quadratic approximation of the function. Consider the normal linear regression model for which the variance estimator $s^2$ possesses a $[\sigma_0^2/(N-K)]\chi_{N-K}^2$ distribution. Asymptotically,

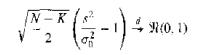
(a) Give an asymptotic approximation for the distribution of $\log s^2/\sigma_0^2$.

(b) Standardize $\log s^2/\sigma_0^2$ so that it is approximately an $\mathcal{N}(0,1)$ random variable and graph its p.d.f., the p.d.f. for $\sqrt{(N-K)/2}[(s^2/\sigma_0^2)-1]$, and the standard normal p.d.f. $N-K=5$, 10, and 20. Which transformation of $s^2$ appears to have the p.d.f. closest to the normal p.d.f.?

N-K N(0.1) 2