Question: (Two-Step and MD) One can apply the minimum distance method to the two-step estimation framework described in Proposition 19 (Two-Step Asymptotic Variance, p. 507). Consider

(Two-Step and MD) One can apply the minimum distance method to the two-step estimation framework described in Proposition 19 (Two-Step Asymptotic Variance, p. 507). Consider the two-step estimator $$\hat{\theta}_N(\hat{\gamma}_N)$$ for a parameter vector $$\theta_0$$ based on the initial estimator $$\hat{\gamma}_N$$ for the nuisance parameter vector $$\gamma_0$$. Among other conditions, we supposed that

N N(20)-60 N 2*] ([22]) -

Thus, given a consistent estimator $$\hat{\Omega}$$ of the variance matrix $$\Omega$$, a minimum distance estimator is

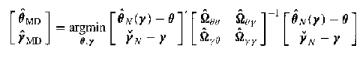image text in transcribed Compare the asymptotic properties of the two estimators.

N N(20)-60 N 2*] ([22]) -

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Econometric Analysis Questions!

Write 2 paragraphs about Macro risks and the term structure of interest rates article. No max word count, page count, or formatting requirements but has to be submit to my tutor's work as my own....

(MD) Reconsider the two-step restricted MD estimator in (24.48). Alternatively, one can reduce the dimension of the first step of estimation by imposing &-0 at that stage as well. (a) Describe the...

Check My Work (1 remaining) LE eBook Marion Health Clinic sees patients on a walk-in basis only. On average, 10 patients per hour enter the clinic. All patients register at the registration window...

Marion Health Clinic sees patients on a walk-in basis only. On average, 10 patients per hour enter the clinic. All patients register at the registration window with a registration clerk (RC), which...

A-Z Marion Health Clinic sees patients on a walk-in basis only. On average, 10 patients per hour enter the clinic. All patients register at the registration window with a registration clerk (RC),...

Marion Health Clinic sees patients on a walk - in basis only. On average, 1 6 patients per hour enter the clinic. All patients register at the registration window with a registration clerk ( RC ) ,...

A Family Health Team clinic sees patients on a walk in basis only. On average, 10 patients per hour enter the clinic. All patients register at the registration window with a registration clerk (RC),...

Paul's Fumiture uses departmental overhead rates (rather than a plantwide overhead rate) to alocate its manufacturing overhead to jobs. The company's two production departments have the foilowing...

The press shown for Prob. 85 has a rated load of 5000 lbf. The twin screws have Acme threads, a diameter of 3 in, and a pitch of in. Coefficients of friction are 0.05 for the threads and 0.06 for...

What is the purpose of the domestic filing exception? To exempt _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ from being required to report certain international tax items. Pass - through entities with more than 5...

The amount absorbed is 0.1 (ct - 0.05) if ct 0.05. The above problem investigates absorption that is not proportional to the concentration in the lungs. Assume = 0.21 and q = 0.1, and find the...