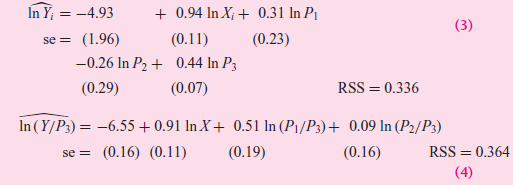Marc Nerlove has estimated the following cost function for electricity generation:

Y = AX^β P^α1 P^α2 P^α3u €¦€¦€¦€¦€¦.. (1)

Where

Y = total cost of production

X = output in kilowatt hours

P₁ = price of labor input

P₂ = price of capital input

P₃ = price of fuel

u = disturbance term

Theoretically, the sum of the price elasticities is expected to be unity, i.e., (α₁ + α₂ + α₃) = 1. By imposing this restriction, the preceding cost function can be written as

(Y/P₃) = AX_β(P₁/P₃)^α1 (P₂/P₃)^α2u €¦€¦€¦. (2)

In other words, (1) is an unrestricted and (2) is the restricted cost function.

On the basis of a sample of 29 medium-sized firms, and after logarithmic transformation, Nerlove obtained the following regression results:

a. Interpret Eqs. (3) and (4).

b. How would you find out if the restriction (α₁ + α₂ + α₃) = 1 is valid? Show your calculations.

In Y; = -4.93 se = (1.96) + 0.94 In X; + 0.31 ln P1 (3) (0.23) (0.11) -0.26 In P2 + 0.44 In P3 (0.07) RSS = 0.336 (0.29) In (Y/P3) = -6.55 + 0.91 In X + 0.51 In (P1/P3)+ 0.09 In (P2/P3) se = (0.16) (0.11) (0.16) RSS = 0.364 %3D (0.19) (4)