Take the model Y X0e with E[Ze] 0, Y 2 R, X 2 Rk , Z 2 R`, ` k. Consider the

Take the model Y Æ X0¯Åe with E[Ze] Æ 0, Y 2 R, X 2 Rk , Z 2 R`, ` ¸ k. Consider the statistic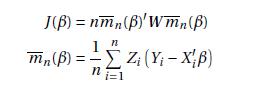

for some weight matrixW È 0.

(a) Take the hypothesis H0 : ¯ Æ ¯0. Derive the asymptotic distribution of J (¯0) under H0 as n!1.

(b) What choice for W yields a known asymptotic distribution in part (a)? (Be specific about degrees of freedom.)

(c) Write down an appropriate estimator cW for W which takes advantage of H0. (You do not need to demonstrate consistency or unbiasedness.)

(d) Describe an asymptotic test of H0 against H1 : ¯ 6Æ ¯0 based on this statistic.

(e) Use the result in part

(d) to construct a confidence region for ¯. What can you say about the form of this region? For example, does the confidence region take the form of an ellipse, similar to conventional confidence regions?

J(B) =nmn(B)'Wmn (B) mn(B) ==Zi (Yi-XB) n