This exercise shows that the sample variance is an unbiased estimator of the population variance when \(Y_{1}, \ldots, Y_{n}\) are i.i.d. with mean \(\mu_{Y}\) and variance \(\sigma_{Y}^{2}\).

a. Use Equation (2.32) to show that \(E\left(Y_{i}-\bar{Y}\right)^{2}=\operatorname{var}\left(Y_{i}\right)-2 \operatorname{cov}\left(Y_{i}, \bar{Y}\right)+\operatorname{var}(\bar{Y})\).

b. Use Equation (2.34) to show that \(\operatorname{cov}\left(\bar{Y}, Y_{i}\right)=\sigma_{Y}^{2} / n\).

c. Use the results in (a) and (b) to show that \(E\left(s_{Y}^{2}\right)=\sigma_{Y}^{2}\).

Equation (2.32)

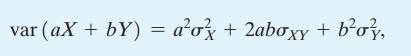
Equation (2.34)

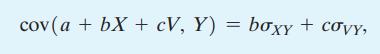
var (ax + bY) = ax + 2abxy + b, 2