Consider an economy that is populated by many identical riskneutral banks so that we can pick up
Question:
Consider an economy that is populated by many identical riskneutral banks so that we can pick up an arbitrary representative bank and investigate its behavior. The bank makes loans at time 0, and the loans mature at time 1. The bank has limited liability. Deposits are insured. The market for deposits is competitive. For simplicity we assume that the market interest rate on insured deposits is zero. Figure 12.14 shows the balance sheets of the bank in period 0 and period 1. The insurance premium is proportional to the level of deposits: \(P=\phi D(\phi>0)\). The premium has to be paid upfront, which means that equity must at least be sufficient to cover the insurance premium, \(E \geq P\).
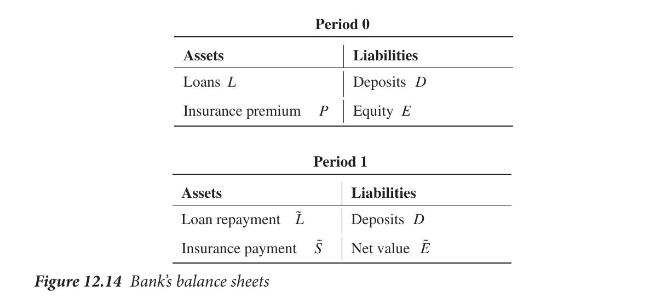
(a) Assume that in period 0 the bank has a given level of equity, \(E\). Use the balance sheet for period 0 to show that
i. If the bank lends \(L\), it needs to collect deposits as much as
\[D=\frac{L-E}{1-\phi}\]
ii. The maximum amount that the bank can lend is \(L^{\max }=\frac{E}{\phi}\).
(b) The payout from the insurance fund is \[\tilde{S}= \begin{cases}0 & \text { if } \tilde{L} \geq D \tag{12.1}\\ D-\tilde{L} & \text { if } \tilde{L}
(c) Suppose the gross repayment on the loans is \((R+\Delta) L\) with probability \(\frac{1}{2}\) and \((R-\Delta) L\) with probability \(\frac{1}{2}\). Assume \(R>1\) and \(R-1
(d) Given the same distribution of \(\tilde{L}\) as in the question (c), what is the expected net profit of the bank's owners? How does it depend on \(\Delta\) and \(L\) ? What general principle(s) does this example illustrate?
(e) Suppose the bank can choose the level of risk, \(\Delta\), and the volume of loans \(L\), freely within the range permitted by the assumptions above. What levels would it choose if it starts with a given equity level \(E\) ? What rate of return on equity would this choice result in? Show that the net rate of return is negative for some parameter values. Why do you think this can be the case?
(f) Will the size of \(\phi\) affect risk taking? If so, in what way?
Step by Step Answer:






