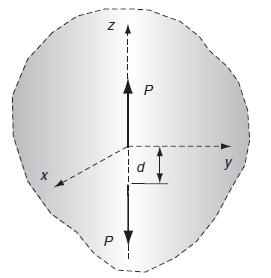
Question: A force doublet is commonly defined as two equal but opposite forces acting in an infinite medium as shown in the following figure. Develop the
A force doublet is commonly defined as two equal but opposite forces acting in an infinite medium as shown in the following figure. Develop the stress field for this problem by superimposing the solution from Example 13.1 onto that of another single force of –P acting at the point z =–d. In particular, consider the case as d→0 such that the product Pd→D, where D is a constant. This summation and limiting process yield a solution that is simply the derivative of the original Kelvin state. For example, the superposition of the radial stress component gives:
![lim [o,(r,z) o,(r,z+ d)] : = OR dor z TRO -d- D 8T (1- - v) dz The other stress components follow in an](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/1/3/6/03065a24f9e562a81705136029745.jpg)
Data from example 13.1



Equation 13.5.9
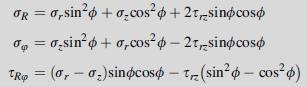
lim [o, (r,z) o,(r,z+d)]: OR dor z = -d- TRO D 8T (1- - v) dz The other stress components follow in an analogous manner. Using relations (13.5.9), show that the stress components in spherical coordinates can be expressed as a -3/2 - [(1 2v)z (r + z)/ 3rz (r + z)5/] (1 + v)D 4 (1 - 1) R-sin+3 (1 + v)D 4T (1 - V) R 2(2-v) +212 +1/200] cos sinocoso
Step by Step Solution
3.40 Rating (156 Votes )
There are 3 Steps involved in it
For the Doublet Force Problem use superposit ion of ... View full answer

Get step-by-step solutions from verified subject matter experts


