Question: Consider a stress function formulation for the axisymmetric problem discussed in Section 14.2. The appropriate compatibility relation for this case has been previously developed in

Consider a stress function formulation for the axisymmetric problem discussed in Section 14.2. The appropriate compatibility relation for this case has been previously developed in Example 8.11; see (8.4.76). Using the plane stress Hooke’s law, express this compatibility relation in terms of stress and then in terms of the Airy function to get the result:

0= d dr2 2011) (2-[(-(-3) (4]

Data from section 14.2

We start our study by re-examining Example 8.6, a plane axisymmetric problem of a hollow cylin- drical domain

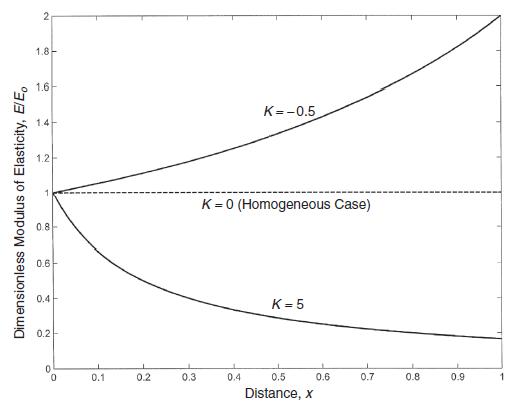
Dimensionless Modulus of Elasticity, E/E, 2 1.8- 1.6 1.4- 1.2 0.8 0.6 0.4 0.2 8 0 0.1 0.2 0.3 K=-0.5 K = 0

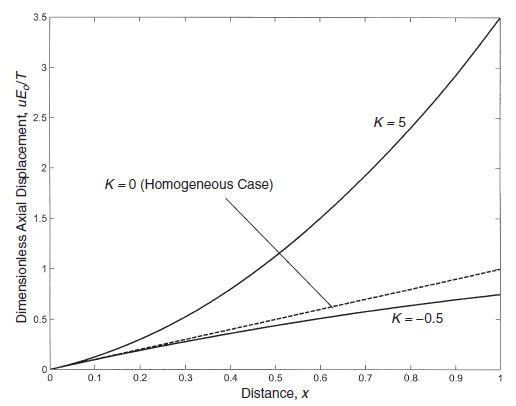
Dimensionless Axial Displacement, uE/T 3.5 2.5 1.5- 0.5- 0 0.1 K = 0 (Homogeneous Case) 0.2 0.3 0.4 0.5

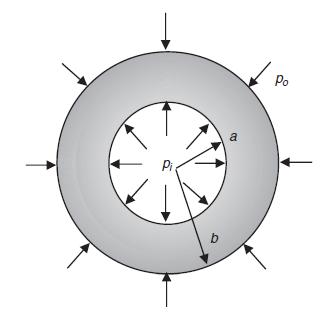
Pi b a Po

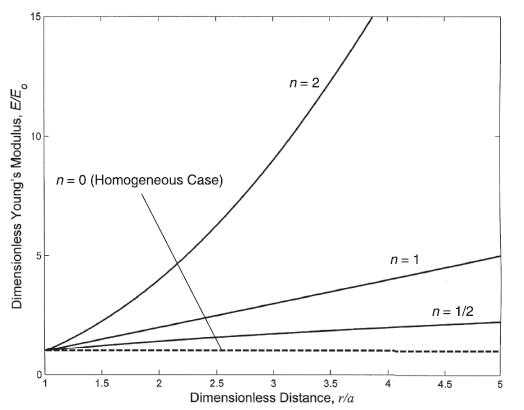
Or = de E(r) [du 1- (r) dr E(r) 1-v(r) +v(r = du [+(r)]) dr Note that the corresponding plane strain

where E, and n are constants and a is the inner boundary radius. Note that Eo has the same units as E and as

Dimensionless Young's Modulus, E/E 15 10 n = 0 (Homogeneous Case) 1.5 2 n=2 2.5 3.5 Dimensionless Distance,

This particular gradation model reduces the Navier equation (14.2.2) to du (n+1) du dr + dr r The solution to

As with the homogeneous example, we choose the special case with only internal pressure (po = 0), which gives

which matches with the solution shown in Fig. 8.9 for bla = 2. A plot of the nondimensional stress

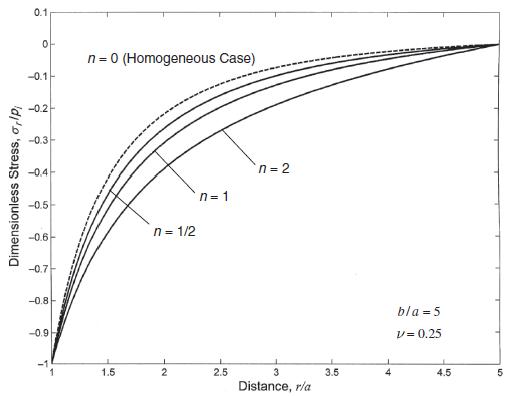
Dimensionless Stress, , p 0.1 of -0.1- -0.2 -0.3 -0.4 -0.5- -0.6- -0.7- -0.8 -0.9 n = 0 (Homogeneous Case)

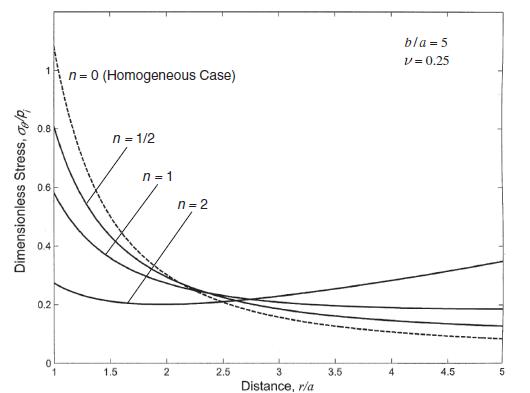
Dimensionless Stress, P 0.8 0.6 0.4 0,2 0 n = 0 (Homogeneous Case) n = 1/2 1.5 n=1 L 2 n=2 2.5 3 Distance,

corresponding results for the tangential stress shown in Fig. 14.8 show much more marked differences. WhileData from example 8.11

As a final example in this section, consider the problem of a thin uniform circular disk subject to constant

y a (0) X

The solution can be efficiently handled by using a special stress function that automatically satisfies the

Recall that the more general polar coordinate case was given as Exercise 7.17. Using Hooke's law for plane

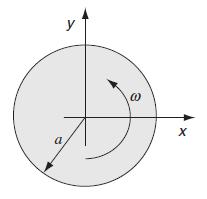
Equation 8.4.76

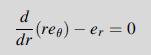
d dr (rea) er = 0 -

0= dr2 d 102 1) (2 -[(-(-3) (4]

Step by Step Solution

★★★★★

3.40 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Hookes Law plane stress e lo 1 E... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Elasticity Theory Applications Questions!

Q:

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Q:

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

Q:

For the torsion problem discussed in Section 14.6, explicitly justify the reductions in polar coordinates summarized by relations (14.6.8) and (14.6.9). Data from section 14.6 Equation 14.6.8...

Q:

Due to the changing environment and external triggers, contingency planning is necessary. What qualities make a future issue a ?trigger?? Consider you are on the strategic planning team for a soft...

Q:

Through the use of strategic alternatives, companies may compete in a marketplace, achieve its vision, or if no vision has been articulated, decide where it might go and what it might achieve....

Q:

Lecture Notes DL MGT 5100 - Distribution Management Spring 2017 1.0. Day one, Monday, Monday, 9 Jan 17 1.1. Reading Assignments: Chapters 1 and 2 1.1.1. I intend to follow the book so as to provide a...

Q:

Lecture Notes DL MGT 5100 - Distribution Management Spring 2017 1.0. Day one, Monday, Monday, 9 Jan 17 1.1. Reading Assignments: Chapters 1 and 2 1.1.1. I intend to follow the book so as to provide a...

Q:

Lecture Notes DL MGT 5100 - Distribution Management Spring 2017 1.0. Day one, Monday, Monday, 9 Jan 17 1.1. Reading Assignments: Chapters 1 and 2 1.1.1. I intend to follow the book so as to provide a...

Q:

Summarize the following chapter in your words: (Basic elements of individual behavior in organizations) What is individual behavior in organization? The people who populate today's business world are...

Q:

HBSP Product Number TCG 333 THE CRIMSON PRESS CURRICULUM CENTER THE CRIMSON GROUP, INC. Note on Strategic DecisionMaking in Healthcare Organizations During the next several decades, healthcare...

Q:

This is based on a book called "Song Of Solomon" by Toni Morrison. Milkman and Guitar are two characters in the novel.

Q:

What is the difference between fusing and sintering?

Q:

How might a retailer use relationship marketing to improve customer loyalty?

Q:

17. Develop a questionnaire for measuring consumer preferences for Italian sausage.

Q:

A trough of concrete weighs 800 lb (Figure P4.17). (a) Draw a free body diagram of the cables ring A. (b) Treating the ring as a particle, determine the tension in cables AB and AC. Figure P4.17 A 30...

Q:

Cable AB on the boom truck is hoisting the 2500-lb section of precast concrete (Figure P4.18). A second cable is under tension P, and workers use it to pull and adjust the position of the concrete...

Q:

Solve the problem of Example 4.5 by using the force components method. Replace the polar representation of the anchor straps tension by the horizontal and vertical components T x and T y , and solve...

Q:

Beta Electronics has a plant assct that cost $45,000 and has accumulated depreciation of $10,000. The plant asset is sold for cash at a $1,000 gain. How much increase in cash flow should Beta report...

Q:

Why do you want a File Server to be its own server and not sharing roles?

Q:

Evaluate the following code. What is the resulting value of the variable a? char a = 56; a &= ~(1